728x90
반응형

인과관계 > 상관관계 > 우연
과학적으로 인정받은 인과관계는 같은 조건 하 미래에도 반복될 수 있는 예측능력이 있음
인과관계의 필수조건
상관관계의 한계점
- 상관관계 분석 자체는 연구방법 / 주제가 맞다면 문제는 없지만, 이를 인과관계로 해석한다면 확대 해석 문제 발생
- 상관관계는 변수 간 강한 연관관계는 알 수 있지만, 그 연관성이 정말 신뢰할 만한 지 검증할 방법이 없음
- 또한 상관관계는 어떤 원인으로 특정 결과가 발생하는지 '예측'하는 욕구를 충족시켜주지 못함
상관관계가 인과관계가 되기 위해 필요한 것
- 반복적 패턴이 발생해야 함
- 시간적 순서가 확보돼야 함
- 실제 논리적으로 설명이 가능해야 함
예시 : 미국 대선 결과와 월드시리즈 우승팀과의 관계
| 연도 | 챔피언이 속한 리그 | 대통령이 된 후보의 정당 |
| 2000 | AL (뉴욕 양키스) | 공화당 (조지 부시) |
| 2004 | AL (보스턴 레드삭스) | 공화당 (조지 부시) |
| 2008 | NL (필라델피아 필리스) | 민주당 (버락 오바마) |
| 2012 | NL (샌프란시스코 자이언츠) | 민주당 (버락 오바마) |
- 첫 번째 조건 만족 : 2000년 이후 부터 4번 연속 반복적 패턴 충족
- 두 번째 조건 만족 : 월드시리즈 최종전은 11월 2일 즈음, 미 대선은 11월 8일에 치러져 원인과 결과 시간 순서 확보
- 세 번째 조건 불만족 : 제3의 변수가 두 사건을 연결할 수 있는 논리가 없음
모델링과 추정
- 추정 : 변수(측정자료) 간의 관계를 규명하는 것
- 모델링 : 변수 간 관계를 추정하기 위한 테스트 / 일반화 작업
- '예측'과 '추정'은 다르다
- 변수 간 '관계를 규명'하는 것이 추정이고, 추정된 방정식에 변수를 대입해 결과값을 찾아내는 게 예측
오류는 모델링의 꽃
- 편차, 오차, 잔차를 포함하는 오류는 분석에 있어 꽃이다 = 오류가 적을 때 예측의 정확성이 높아지기 때문
오류의 구분 : 일종오류와 이종오류
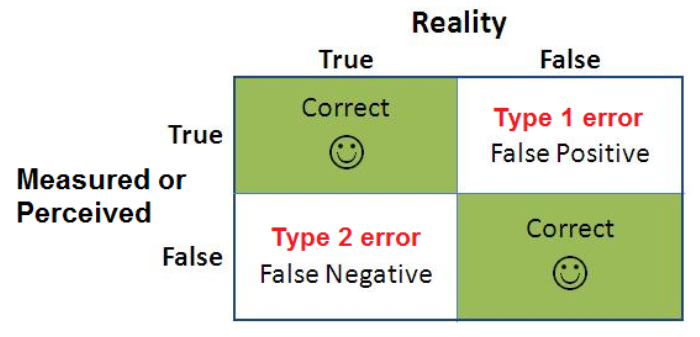
- 일종오류 (긍정오류) : 사실이 아니지만 그 값이 사실이라고 하는 경우
- ex) 암에 걸리지 않은 환자(False)에게 암 판정(True)을 내리는 경우
- 이종오류 (부정오류) : 사실이지만 그 값이 사실이 아니라고 하는 경우 (좀 더 위험할 수 있음)
- ex) 지뢰가 있는데(True) 지뢰가 없다고(False) 하는 경우
진실이 존재하는 신의 영역
- 모집단의 규모가 커지수록 모집단의 평균을 알아내는 것은 불가능
- 변수 간 관계에 눈에 보이지 않는 영향을 미친 잠재 변수가 있을 수 있음 (=신의 영역)
- ex) 몸무게와 장타율 관계 : 장타율에 몸무게 말고도 영향을 미친 잠재 변수가 있을 수 있음

예측모델과 데이터가 있는 현실계
- 전체 데이터를 모은다는 것은 현실적으로 불가능한 경우가 대부분, 가능하다고 해도 많은 비용과 시간 소요
- 데이터가 일정 수준 모이면, 추가 데이터가 통계검증에 큰 차이를 내지 않음
- 따라서 모집단에서 편향 없는 표본추출을 통해 표본 데이터를 모으고, 기울기와 절편 오류항을 추정하는 방식 선택
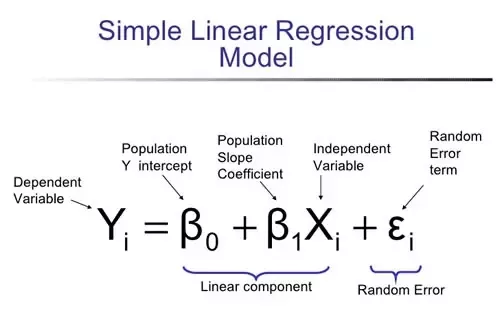
- Yi (또는 Y hat)는 예측모델에서 나온 예측값
- 편차 : 각 변수값이 평균으로부터 떨어져 있는 정도, 집합의 편차는 항상 0
- 표준편차(RMSE) : 편차제곱의 합에 다시 제곱근을 한 것, 표준편차(오류)가 작을수록 예측이 정확할 확률이 높다.
실습
- 2011년부터 2016년까지 시즌 150경기를 초과 출장한 선수를 대상으로 체중 - 장타율 회귀분석
library(Lahman)
a<-subset(Batting, yearID>2010 & yearID<2017 & G>150)
b<-subset(People, sel=c('playerID', 'weight'))
c<-merge(a,b,by='playerID')
c$slg<-with(c,((H-X2B-X3B-HR)+2*X2B+3*X3B+4*HR)/AB)
with(c,plot(weight,slg,type='n'))
abline(lm(slg~weight, c))
fit<-lm(slg~weight, c)
fit_res<-resid(fit)
plot(c$weight, fit_res)
abline(0,0)
qqnorm(fit_res)
qqline(fit_res)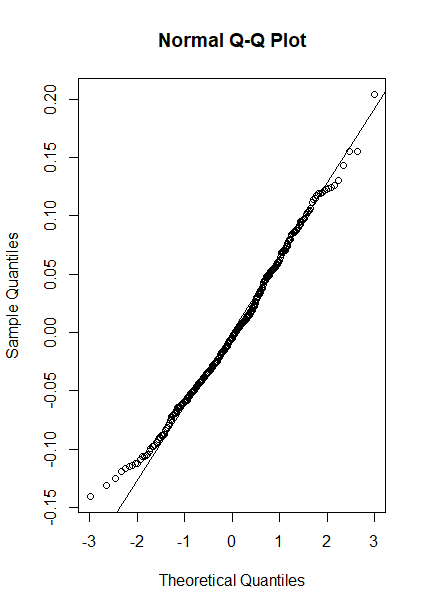
- 잔차 : 추정모델에 독립 변수를 넣고 구한 예측값과 실제 관측값의 차
- 잔찻값이 크면 클수록 추정된 예측선의 예측능력이 떨어짐
- RSS : 예측선으로 설명되지 못하는 범위의 합
- TSS : 전체 좌승의 합
- ESS : 설명되는 부분의 합
- R^2 : 설명력

728x90
'Minding's Reading > 메이저리그 야구 통계학 2e' 카테고리의 다른 글
| [메이저리그 야구 통계학 2/e] 4장 - 상관관계는 인과관계가 아니다(3) (0) | 2023.05.10 |
|---|---|
| [메이저리그 야구 통계학 2/e] 4장 - 상관관계는 인과관계가 아니다(2) (2) | 2023.05.08 |
| [메이저리그 야구 통계학 2/e] 3장 - 선수의 능력은 어떻게 측정할 것인가?(2) (0) | 2023.04.25 |
| [메이저리그 야구 통계학 2/e] 3장 - 선수의 능력은 어떻게 측정할 것인가?(1) (0) | 2023.04.24 |
| [메이저리그 야구 통계학 2/e] 2장 - 메이저리그 데이터 마이닝 (2) | 2023.04.20 |