728x90
반응형

데이터에서 룰을 찾다 : 연관성 분석
- 분석할 데이터에서 패턴과 연관성을 잘 파악하면 마케팅 등 전략에 활용할 여지가 많음
연관성 분석
- 연관성 분석은 변수 내 개별 관측자료가 여타 관측자료와 어떻게 어울리는지 파악하는데 주력
- ex) 이적시장에서 특정 팀 출신의 선수를 전략적으로 선호하는가?
# 전처리
library(Lahman)
a <- subset(Batting, yearID>2010&yearID<2016, select=c(playerID, teamID))
a$teamID <- factor(a$teamID)
a$teamID <- as.character(a$teamID)
# dcast()를 통해 동일 playerID를 갖는 소속팀 정보를 동일한 하나의 행으로 변경
library(data.table) # dcast()를 사용하기 위해서 패키지 필요
move <- dcast(setDT(a)[,idx := 1:.N, by = playerID],
playerID~idx, value.var=c('teamID'))
move[is.na(move)]<-''
move[,1]<-NULL
write.csv(move,file='move.csv') # 파일을 csv로 저장# read.transactions() : 저장된 파일을 R로 불러들일 때 사용
library(arules)
move <- read.transactions('move.csv', sep=',')summary(move)
>>>
transactions as itemMatrix in sparse format with
2326 rows (elements/itemsets/transactions) and
2356 columns (items) and a density of 0.001176995
most frequent items:
NYA CHN TOR BOS TEX (Other)
165 158 158 157 153 5659
element (itemset/transaction) length distribution:
sizes
2 3 4 5 6 7 8 9
1260 596 289 121 46 9 3 2
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.000 2.000 2.000 2.773 3.000 9.000
includes extended item information - examples:
labels
1 1
2 10
3 1002011년부터 시작되는 관츤기간 동안 뉴욕 양키스에서 활동한 선수의 빈도가 가장 높다는 사실 확인
관측 기간동안 무려 9개 팀에서 활약한 선수도 있다는 것을 알 수 있다.
# 막대그래프 시각화
itemFrequencyPlot(move, support=0.01,cex.names=0.6)
# apriori로 선수들 팀 간 이동패턴 찾기
pattern <- apriori(move, list(support=0.0015, confidence=0.50, minlen=2))
summary(inspect(pattern))
>>>
lhs rhs support confidence
[1] {FLO} => {MIA} 0.01074807 0.5681818
[2] {FLO, LAN} => {MIA} 0.00171969 1.0000000
[3] {NYA, PHI} => {PIT} 0.00171969 0.5000000
coverage lift count
[1] 0.018916595 10.744642 25
[2] 0.001719690 18.910569 4
[3] 0.003439381 8.551471 4
lhs
Length:3 Length:3
Class :character Class :character
Mode :character Mode :character
rhs support confidence
Length:3 Min. :0.001720 Min. :0.5000
Class :character 1st Qu.:0.001720 1st Qu.:0.5341
Mode :character Median :0.001720 Median :0.5682
Mean :0.004729 Mean :0.6894
3rd Qu.:0.006234 3rd Qu.:0.7841
Max. :0.010748 Max. :1.0000
coverage lift count
Min. :0.001720 Min. : 8.551 Min. : 4.0
1st Qu.:0.002580 1st Qu.: 9.648 1st Qu.: 4.0
Median :0.003439 Median :10.745 Median : 4.0
Mean :0.008025 Mean :12.736 Mean :11.0
3rd Qu.:0.011178 3rd Qu.:14.828 3rd Qu.:14.5
Max. :0.018917 Max. :18.911 Max. :25.0FLO(플로리다 말린스)에서 MIA(마이애미 말린스)로 팀명이 바뀌면서 선수들이 이동한 패턴이 1, 2위를 차지했다.
그 부분을 제외하면 NYA(뉴욕 양키스)와 PHI(필라델피아 필리스)에서 활약한 선수들이 PIT(피츠버그 파이어리츠)로
이동하는 패턴이 많이 발생했다. 발생건수는 총 4건.
그러나 2325건의 선수 이동 패턴 중 단 4건은 0.0017에 해당해 유의미한 패턴이라고 보기는 어렵다.
쇼핑몰이나 넷플릭스 등 충분히 패턴을 가질 수 있는 환경에서는 2%에 해당될 정도로 중요하게 여겨야 할 사례가 있음
선수와 감독의 인적 상관성 : 네트워크 분석
- 사람으로 구성도니 사회에서 지식, 혁신, 뉴스 등은 사람의 네트워크인 인맥을 통해 전달됨
- 최근은 SNS를 통해 인터넷으로 더 빠르게 확산
- 야구 또한 선수, 감독, 직원, 스카우터 등을 통해 다른 팀의 전략이 쉽게 모방/학습되는 스포츠 중 하나
- 네트워크 분석을 통해 연결망을 분석할 수 있음
네트워크 분석을 통해 팀의 에이스급 투수들이 어떤 관계망을 흔들었는지 분석
- '15 ~ '16시즌 동안 감독의 교체가 있었거나 에이스급 투수들의 이동이 있었다면 관계망이 생김
- 그렇지 않다면 독립된 그룹을 가짐
- 중요한 인적자원의 이동이 해당 팀에 영향을 미칠 가능성이 높기때문에, 관계망을 맺는 그룹 간 전략 유사성이 있을 것
# 전처리
# 35경기 이상 출장한 투수
a <- subset(Pitching, yearID>2014&yearID<2017&G>35, select=c('playerID','yearID','teamID'))
a$yearID <- str_remove(a$yearID, '20')
a$teamyear <- paste(a$teamID, a$yearID, sep='') # paste()를 통해 두 글자를 합침
b <- subset(Managers, yearID>2014&yearID<2017, select=c('playerID', 'yearID', 'teamID'))
b$yearID <- str_remove(b$yearID, '20')
b$teamyear <- paste(b$teamID, b$yearID, sep='')
c <- merge(a,b,by='teamyear')
d <- subset(c, select=c('playerID.x', 'playerID.y')) # 같은 시기에 활동했던 투수와 감독을 짝지음
colnames(d) <- c('pitcher_ID', 'manager_ID')# 네트워크 시각화
library(igraph)
mlb_network <- graph.data.frame(d, directed = FALSE)
V(mlb_network)$label <- ifelse(V(mlb_network)$naem %in% c(b$playerID)>0,
as.character(b$teamyear), NA)
mlb_network
>>>
IGRAPH b4af481 UN-- 312 468 --
+ attr: name (v/c), label (v/c)
+ edges from b4af481 (vertex names):
[1] zieglbr01--halech01 collmjo01--halech01
[3] chafian01--halech01 perezol01--halech01
[5] hudsoda01--halech01 hernada01--halech01
[7] delgara01--halech01 reedad01 --halech01
[9] zieglbr01--halech01 burgoen02--halech01
[11] clippty01--halech01 barreja01--halech01
[13] delgara01--halech01 hudsoda01--halech01
[15] corbipa01--halech01 cunnibr02--gonzafr99
+ ... omitted several edges이름과 라벨이 준비됐다.
manager <- V(mlb_network)$name %in% c(b$playerID)+1
plot(mlb_network, vertex.shapes='none', vertex.label.cex=1.5, vertex.label.color='black',
vertex.label.font=2, vertex.label.dist=1,
vertex.size=c(3,0)[manager], vertex.color=c('gray', 'white')[manager])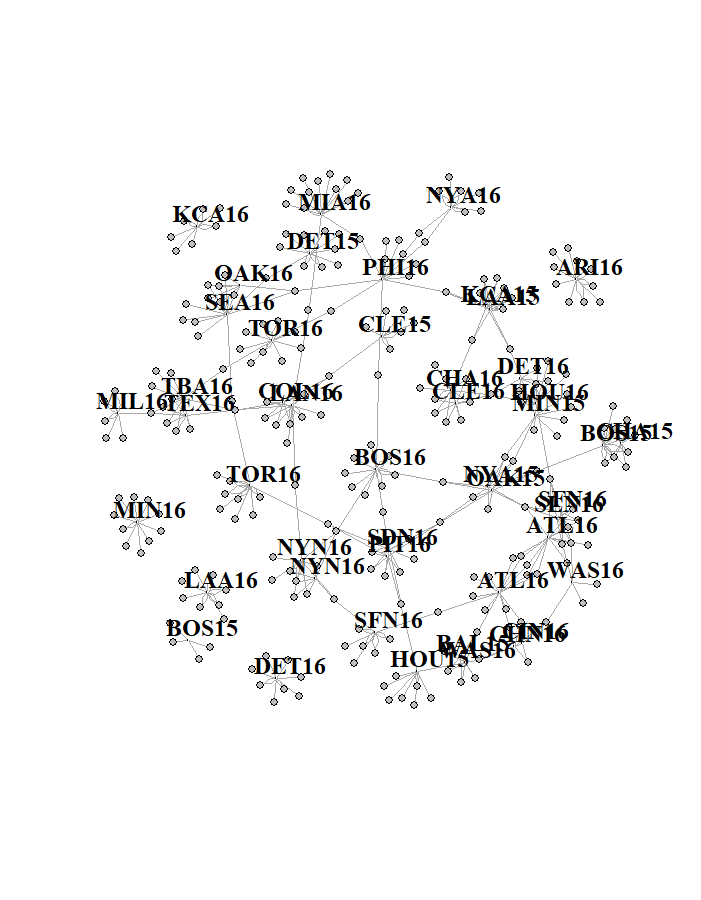
기술통계와 추정통계의 매개: 히스토그램은 막대그래프가 아니다
- 히스토그램 : 변수의 분산 정도와 변수에 있는 사건들이 발생하는 정도를 보여주는 시각화 자료
- 단순히 팀 별 홈런 수를 보여주는 막대그래프와는 다른 모습을 가지고 있다.
library(Lahman)
a <- subset(Teams, yearID==2015)
b <- barplot(a$HR)
text(b,par('usr')[3], labels=a$teamID, srt=60, adj=c(1,0.5),xpd=TRUE)
# par('usr')[3] : 팀 이름의 위치를 차트 아랫부분에 두겠다는 옵션 / [4]는 맨 위에 위치
# srt=60은 팀 이름을 60도로 기울인다는 뜻
히스토그램
- 특정 사건이 발생한 확률을 시각적으로 보여주는 기술통계
- 모집단의 특성을 추정하는 데 필요한 확률분포를 제시해주는 추정통계의 이론적 기반
# 데릭 지터의 홈런 분포를 히스토그램으로 그려보기
a <- subset(Batting, playerID=='jeterde01')
# hist(분석 대상 변수 위치, x축 이름, 차트의 제목, 차트의 눈금 숫자에 대한 방향조절)
hist(a$HR, xlab='Homerun', main='Histrogram of Jeter's HR', las=1)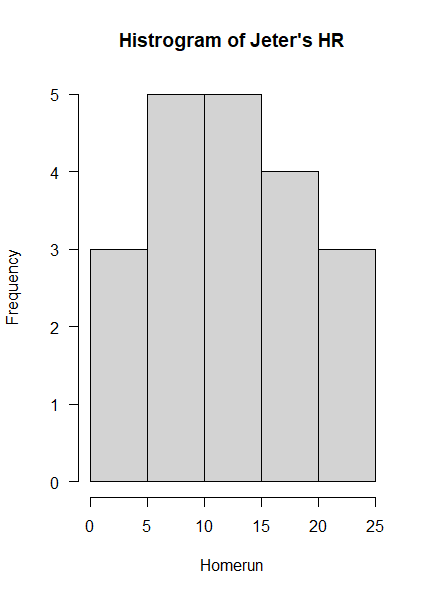
데릭 지터는 대체적으로 5개에서 15개 사이의 시즌 홈런을 기록했다는 것을 알 수 있다.
평균을 중심으로 빈도가 줄어드는 정규분포 형태를 닮아있다. (사건 수가 더 많았다면, 정규분포 형태를 띄었을 것)
728x90
'Minding's Reading > 메이저리그 야구 통계학 2e' 카테고리의 다른 글
| [메이저리그 야구 통계학 2/e] 4장 - 상관관계는 인과관계가 아니다(2) (2) | 2023.05.08 |
|---|---|
| [메이저리그 야구 통계학 2/e] 4장 - 상관관계는 인과관계가 아니다(1) (0) | 2023.05.01 |
| [메이저리그 야구 통계학 2/e] 3장 - 선수의 능력은 어떻게 측정할 것인가?(1) (0) | 2023.04.24 |
| [메이저리그 야구 통계학 2/e] 2장 - 메이저리그 데이터 마이닝 (2) | 2023.04.20 |
| [메이저리그 야구 통계학 2/e] R 설치, R Studio(Posit) 설치 (0) | 2023.02.06 |