728x90
반응형

확률과 우도
확률 (Probability)
- 동전 던지기의 경우, 나올 수 있는 상황이 앞면과 뒷면 두 가지다.
- 두 가지 중 한 가지 상황을 성공이라고 가정할 때, 시도가 많으면 많을수록 50%에 가까워지게 됨
- 야구 또한 타율, 출루율 등을 통해 타자의 안타 여부 / 출루 여부의 확률을 예측함
조이 보토의 출루율 예시
- 조이 보토는 타출갭(타율 - 출루율 간 차이)이 뛰어난 선수로 알려져 있다.
- 그의 출루율이 .460이라면, 5타석 중 2번 출루할 확률을 얼마나 되는가?
- 출루의 경우 성공과 실패 두 가지 결괏값을 가지는 이항분포다.
- 이항분포가 여러 번 시행된 결괏값 집합이라면, 베르누이 분포의 공식으로 성공/실패 가능성 제시 가능하다.

- 여기서 p는 특정사건이 발생할 가능성이다. 즉, p(x)는 x라는 사건이 발생할 가능성인 것.
- x는 사건이 발생한다고 가정했을 때 1, 그렇지 않으면 0을 대입한다.
- 각 타석마다 베르누이 분포가 발생한다.
베르누이 분포로 구성된 이항확률분포를 구하는 두 가지 방법
1. 수학적으로 구하는 방법
- 이항확률밀도함수에 출루율과 시행횟수를 대입해서 구하는 방법
- nCr * p^r * (1-p)^(n-r)
- n은 총 타석수, r은 몇 번 출루했을 때를 가정하는 지, p는 성공확률이다.
- .460의 출루율을 가진 선수가 5타석 중 2번 출루할 확률은 33.32%
2. 시뮬레이션 접근법
- 시뮬레이션을 돌릴 횟수, 타석수, 출루율을 지정해줘야 함
a <- rbinom(10000, 5, 0.46) # 10000번의 시뮬레이션, 5타석, .460의 출루율
table(a)/10000
>>>
a
0 1 2 3 4 5
0.0416 0.1905 0.3406 0.2839 0.1236 0.0198- 시뮬레이션 결과 2번 출루할 확률이 가장 높으며, 그 확률은 34% 정도다.
- 이항확률밀도함수의 결과와 비슷한 값을 가짐
- 시뮬레이션 횟수가 높을수록 변동성이 낮아지며 안정적인 결과를 얻을 수 있다.
출루의 조건 : 최대우도추정법
- 우도의 개념을 이용해 모수를 역추적하는 분석기술은 상당한 관심을 받고 있음
- 특정 사건의 발생확률을 최대화할 수 있는 조건들을 데이터를 통해 역추적 & 모수 특징 파악
- 사건 발생 예측하고 미연에 방지하도록 도움을 주는 모델 개발 가능
- 이처럼 특정 사건의 확률 최대화할 수 있는 파라미터를 찾기 위해 이항확률밀도함수를 역으로 이용하는 방법이 최대우도추정법
- ex) 로지스틱 회귀분석
조이 보토의 출루율이 알려져 있지 않다면?
- 만약 5번의 타석 중 2번 출루할 수 있는 확률을 극대화하는데 필요한 출루율을 4할이라고 역추적했다면
- 4할이라는 수치는 5C2의 확률을 극대화하는 우도(likelihood)가 된다.
확률과 우도가 다른 점
- 확률은 한 사건의 조건인 출루율을 알고 있어서 5타석 중 2출루가 발생할 빈도에 주목 가능
- 그러나 출루율을 모르는 경우엔 5타석 중 2출루가 발생할 가장 높은 조건을 찾아야 하며, 그 조건이 우도

확률 계산과의 비교
- .460의 조이 보토가 5타석 중 2출루할 이론적 확률값은 33.32%, 시뮬레이션 결과는 34%였다.
- 거꾸로 5번의 타석 중 2출루할 가능성을 가장 높이는 출루율 모수를 찾아야 한다.
- 이항확률밀도함수에 전체 시행수인 5(타석)와 성공횟수인 2(출루)를 대입한다.
- P(x) = 5C2 * OBP^2 * (1-OBP)^3
- 위 공식에 로그함수를 적용하면 로그의 특성을 활용해 확률의 최대점을 알 수 있다.
- 로그는 급격히 증가하다가 최댓값에 도달 시 더 이상 증가하지 않는 특성을 가지고 있기 때문

- 그래프의 최대점은 0.4 즉, 출루율 4할이다.
시나리오 확률분포 확인
- 5타석의 뜻은 다섯 번의 시행을 거쳤으며, 0출루 ~ 5출루의 경우까지 6가지 상황마다 다른 확률을 가지게 됨
OBP <- 0.4 # 출루율 4할
base <- 0:5 # 0 ~ 5까지 6가지 케이스
P <- OBP^base*(1-OBP)^(5-base) # 확률계산
case<-choose(5, base)
EV <- P*case
EV
>>>
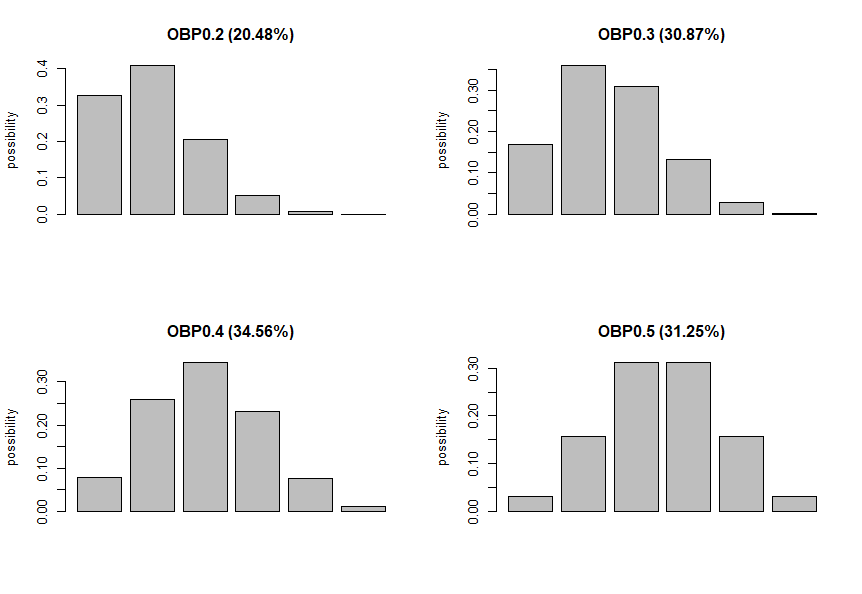
[1] 0.07776 0.25920 0.34560 0.23040 0.07680 0.01024- 2출루할 확률이 34.56%로 가장 높다.
barplot(EV)
이항분포에서 분포의 모양을 정하는 원인
- 선수의 출루율(성공확률)과 시행횟수가 확률분포 모양을 정함
- 출루율에 따라 확률분포모양이 달라지는 모습
728x90
'Minding's Reading > 메이저리그 야구 통계학 2e' 카테고리의 다른 글
| [메이저리그 야구 통계학 2/e] 4장 - 상관관계는 인과관계가 아니다(3) (0) | 2023.05.10 |
|---|---|
| [메이저리그 야구 통계학 2/e] 4장 - 상관관계는 인과관계가 아니다(1) (0) | 2023.05.01 |
| [메이저리그 야구 통계학 2/e] 3장 - 선수의 능력은 어떻게 측정할 것인가?(2) (0) | 2023.04.25 |
| [메이저리그 야구 통계학 2/e] 3장 - 선수의 능력은 어떻게 측정할 것인가?(1) (0) | 2023.04.24 |
| [메이저리그 야구 통계학 2/e] 2장 - 메이저리그 데이터 마이닝 (2) | 2023.04.20 |



