
과학적 측정
- 야구는 팀의 조화가 중요한 다른 스포츠(축구, 농구)보다 선수 개인 능력이 승리에 미치는 영향이 월등히 큼.
- 야구 뿐 아니라 다양한 분야에서 평가 및 가치를 측정하는 직업들이 존재
- 전문성의 기준은 무엇인가?
- 전문가 집단의 진입장벽 (ex. 시험 등)
- 경험이 쌓이며 대상을 볼 줄 아는 안목, 통찰력, 노하우 등
- 전문적 지식이 과학적 지식은 아님
- 경험과 노하우가 쌓이면서 모든 사건에 균등한 관심보다는 특정 사건에 집중하는 선택적 관심을 가지기 때문
- 전통적인 스카우터가 홈런 등 기본 툴에 집중하고 출루율, 볼넷 등을 가볍게 보는게 그 예시
- 선택적 관심의 벽을 넘어 데이터 입수 / 분석 / 해석 능력이 있다면, 비전문가도 의사결정이 가능
측정의 신뢰도
- 누가 평가했느냐보다는, 모든 요인을 고려하는 균등 관심에 기반한 신뢰성과 타당성이 확보돼야 함
- 측정도구의 신뢰도 : 능력을 측정하는 도구가 객관성을 갖고 있음을 의미
- 측정 결과가 평가자와 시점에 관계없이 비슷해야 신뢰도가 높음
- 측정값 = 진정한 능력 + 측정오류
- 신뢰도를 평가하는 기준은 일관성
- 그러나 아무리 신뢰도가 높은 지표라도 측정 오류가 있음
- 측정오류 = 체계적 편향 + 비체계적 분산
- 비표본오차 : 사람을 대상으로 하는 조사방법에서 관측시기, 관측담당자 등에 따라 측정결괏값이 비일치
- 편향성 : 진정한 값을 둘러싸고 체계적으로 잘못 측정하고 있는 것
- 분산 : 측정방식은 정상이지만 응답자의 반응이 조금씩 다른 비체계적 측정오류

- 측정지표의 분산 정도와 편향을 확인하기 위한 방법
- 검증 재검증(test-retest) : 한 명의 평가자가 일정 시간을 두고 같은 선수를 반복적으로 평가
- t-1 시점과 t 시점의 상관관계를 확인하는 방식
- 검증 재검증 방식 실습 (Lahman 데이터 활용)
- 검증 재검증(test-retest) : 한 명의 평가자가 일정 시간을 두고 같은 선수를 반복적으로 평가
library(Lahman)
a<-subset(Batting,yearID==2014)
b<-subset(Batting,yearID==2015)
c<-merge(a,b,by='playerID')
d<-c[c$AB.x>10 & c$AB.y>10,] # x(=2014)와 y(=2015)로 연도를 구분
# 상관관계 계산
with(d, cor(HR.x, HR.y)) # 홈런의 상관계수
>>> 0.6804912
with(d, cor(H.x/AB.x, H.y/AB.y)) # 타율의 상관계수
>>> 0.48685652014년과 2015년 홈런과 타율의 상관관계를 살펴본 결과, 홈런이 타율보다 상관관계가 높다.
즉, 개인홈런 변수보다 개인타율 변수가 신뢰성 있다고 해석할 수 있다.
측정의 타당도
측정지표의 타당성 : 이론의 개념과 그 개념을 측정하는 지표의 일치 정도
- 타자의 능력을 '타율'이라는 지표로 사용할 수 있는 근거
- 타율(안타)은 타자의 능력을 'Run'을 연장하는 응력이라는 개념으로 정의했기 때문
- 'Run'을 가장 쉽게 연장할 수 있는 대표적인 방법이 안타이며, 타석 대비 표준화한 타율은 목적에 맞게 측정
- 여기서 'Run'은 베이스와 베이스 간 개념적 거리, 장타율의 개념을 생각하면 된다. (1루타는 1, 홈런은 4)
- 과학적 방식의 연구는 개념의 측정이 가능해야 한다.
- 구성개념을 명료하게 정의하는 작업이 연구 전 필요함
측정을 시작하기 전에 스스로에게 해야하는 질문 3가지
1. 구성개념이 다르게 해석될 여지는 없는가?
2. 의도된 구성개념을 측정할 수는 있는가?
3. 측정도구는 구성개념을 정확히 반영하는가?
- (구성개념은 과학적 연구방법이나 논리적인 이론에 근거하여 이를 설명하기 위하여 조작적으로 만들어 낸 개념)
능력과 운의 결과물 : 시즌 성적
좋은 능력을 가진 선수를 정확하게 측정해내는 구단은 저비용으로 승리를 구입할 수 있지만, 좋은 능력이 반드시 좋은 성적으로 연결되는 것은 아님.
- 성적(Performance) = 설명되는 능력(Ability) + 설명되지 않는 운(Luck)
- 여기서 '운'은 선수의 능력과 별개로 성적에 영향을 미치는 요소.
- 즉, 분석자 입장에서는 패턴 파악에 도움이 되지 않는 노이즈다.
정확도가 100%가 아니기 때문에, 해당 예측 모델은 실패한 것일까? 그렇다고 볼 수는 없다.
하지만 노이즈를 최대한 줄이고 신호(signal) 부분을 높이는 노력이 필요하다.
노이즈를 줄이면서 신호를 높일 수 있는 두 가지 방법
1. 신뢰성과 타당성이 높은 지표를 사용해야 한다.
- 신뢰성이 좋아 내년에도 반복될 확률이 높은 지표 중 성적과 구성타당도가 높아 성적에 직접적으로 영향을 주는 지표
- 일반적으로 타율, 타점, 득점 등으로 선수의 능력을 평가. 그러나 하위개념(타율)과 겹치는 부분이 많아 한계가 있음
- 결국 타점과 득점을 올리려면 안타를 쳐야하고, 진루에 도움이 된 안타는 기록될 수 없다는 한계도 있음
- 이 한계점을 극복하기 위해 출루율이나 OPS를 사용하기 시작
2. 세상의 모든 현상은 다 측정할 수 있다는 헛된 생각에서 벗어나기
- 타율, 출루율 등과 달리 심리적 상태, 성향, 자아효능감, 팀과의 관계 등은 측정할 수 없음
- 측정할 수는 없지만 분명히 성적에 영향을 미치는 요소
- 측정가능한 모든 변수를 모델에 집어넣는 것도 좋은 것만은 아님 -> 오버피팅 문제 발생 가능
공격지표를 이용한 상관관계
변수 간 관계를 보여주는 대표적인 분석 방법
1. 상관관계 분석
- 다른 변수 간의 연관성을 보여준다.
- 기호는 r, 상관계수라고 부름
- 상관계수는 두 변수가 같이 만들어내는 공통된 분산을 분자로,변수의 표준편차의 전체범위를 분모로 둠
- 상관계수가 1에 가까울수록 정비례 / -1에 가까울수록 반비례관계
2. 인과관계 분석
새로운 구단으로 옮기기 전과 옮긴 후의 타점 간의 상관관계 비교
전처리
# 전처리
library(Lahman)
library(dplyr)
library(plyr)
data <- subset(Batting.yearID>2014&yearID<2017) # 2015 ~ 2016년의 데이터
data$teamID <- as.character(data$teamID)
data$playerID <- as.character(data$playerID)
a <- arrange(data,playerID,yearID) # playerID와 yearID 기준으로 정렬# 각 데이터가 동일선상에 위치하도록 작업(sapply)
a$p_teamID <- as.character(sapply(1:nrow(a), function(x){a$teamID[x-1]}))
a$p_playerID <- as.character(sapply(1:nrow(a), function(x){a$playerID[x-1]}))
a$p_RBI <- as.numeric(sapply(1:nrow(a), function(x){a$RBI[x-1]})) # 타점
a$p_AB <- as.numeric(sapply(1:nrow(a), function(x){a$AB[x-1]})) # 타수
a$p_SF <- as.numeric(sapply(1:nrow(a), function(x){a$SF[x-1]})) # 희생플라이
a$p_SH <- as.numeric(sapply(1:nrow(a), function(x){a$SH[x-1]})) # 희생번트
a$p_H <- as.numeric(sapply(1:nrow(a), function(x){a$H[x-1]})) # 안타
a$same_person <- ifelse(a$playerID == a$p_playerID, 'same', 'different')
b <- a[a$same_person == 'same',] # same표시가 있는 동일선수만 남도록
b$moved <- ifelse(b$teamID == b$p_teamID, 'no', 'yes')
c <- b[b$moved == 'yes',] # 이적선수만 남도록c$p_avg <- with(c,p_H/p_AB) # 2015타율
c$sac <- with(c,p_SF+p_SH) # 2015 희생타
d <- subset(c, AB>400&p_AB>400) # 400타석 이상의 선수들만 포함
d$change_rbi <- with(d, RBI/p_RBI)# 전년도 타율과 타점 변화 간 상관관계
with(d, cor(p_avg, change_rbi))
>>>
[1] -0.4890067전년도 타율과 타점 변화 간 상관계수는 마이너스.
전년도 타율이 높을수록 그 다음 연도 공격능력이 더 높아질 확률은 적다.
시각화
library(ggplot2)
ggplot(d, aes(p_avg, change_rbi, lgID))+geom_point(size=2, aes(shape=lgID))+
annotate('text', x=0.3, y=1.6, label='r=-0.49', size=5)+
stat_smooth(method='lm', col='black')+
labs(x='Batting Avg of Prior Year', y='Change in RBI')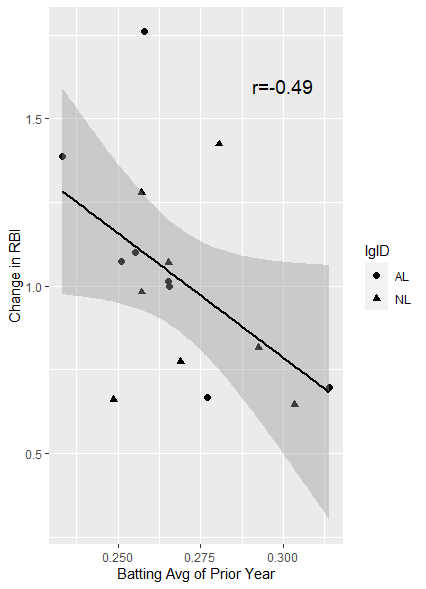
# 리그 별로 독립분석
ggplot(d, aes(p_avg, change_rbi))+geom_point(size=2)+
stat_smooth(method='lm', col='black')+facet_wrap(~d$lgID)+
labs(x='Batting Avg of Prior Year', y = 'Change in RBI')
이전 시즌의 타율이 높을수록 타점은 줄어드는 현상을 볼 수 있다.
# 희생번트와 희생플라이를 많이 친 선수들이 이적 첫 연도에 만들어낸 타점
with(d, cor(sac, change_rbi))
>>>
[1] 0.5042151희생번트와 희생플라이가 타점 변화에 생각보다 높은 상관계수를 나타내고 있다.
# 시각화
ggplot(d, aes(sac, change_rbi, lgID))+geom_point(size=2, aes(shape=lgID))+
annotate('text', x=4, y=1.6, label='r=0.50', size=5)+
stat_smooth(method='lm', col='black')+
labs(x='Sacrifice Flies & Hits', y='Change in RBI')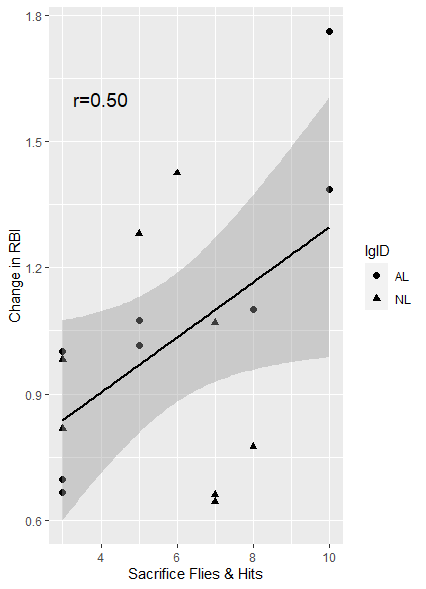
전년도 희생타가 많은 선수가 새로운 팀에 이적했을 때 타점의 상승률도 높다는 것을 알 수 있다.
상관관계표
- 상관관계 분석은 변수 간의 관계 강도에 대한 힌트를 줄 뿐 신뢰성의 판단 기준은 제공하지 않음
- 추가 분석을 진행하기 위한 기초 정보로 활용하면 좋음
- 대부분의 연구는 모든 변수 간의 상관관계를 확인할 수 있는 상관관계표가 요구됨
# 상관관계표
install.packages(tableHTML)
library(tableHTML)
e <- with(d, data.frame(change_rbi, sac, p_avg)) # d에 있는 변수 중 3개를 가져옴
colnames(e) <- c('C_RBI', 'Sac', 'AVG')
cor(e)
>>>
C_RBI Sac AVG
C_RBI 1.0000000 0.5042151 -0.4890067
Sac 0.5042151 1.0000000 -0.4597213
AVG -0.4890067 -0.4597213 1.0000000
'Minding's Reading > 메이저리그 야구 통계학 2e' 카테고리의 다른 글
| [메이저리그 야구 통계학 2/e] 4장 - 상관관계는 인과관계가 아니다(1) (0) | 2023.05.01 |
|---|---|
| [메이저리그 야구 통계학 2/e] 3장 - 선수의 능력은 어떻게 측정할 것인가?(2) (0) | 2023.04.25 |
| [메이저리그 야구 통계학 2/e] 2장 - 메이저리그 데이터 마이닝 (2) | 2023.04.20 |
| [메이저리그 야구 통계학 2/e] R 설치, R Studio(Posit) 설치 (0) | 2023.02.06 |
| [메이저리그 야구 통계학 2/e] 책 읽기 전 변수 개념 정리 (0) | 2023.02.01 |