728x90
반응형

정규분포 : 얼마나 칠 것인가?
- 타율 / 출루율 / 장타율 등 연속형 변수들은 데이터 상호독립성을 띄고 있기 때문에 평균을 중심으로 정규분포를 구성
- 홈런 / 타점 등 이산형변수도 데이터가 충분하다면 중심극한정리에 기반해 정규분포의 모양을 띤다고 할 수 있음
중심극한정리?
동일한 확률분포를 가진 독립 확률 변수 n개의 평균의 분포는 n이 적당히 크다면 정규분포에 가까워진다는 정리
- 중심극한정리는 연속형 변수 및 이산 변수에 데이터 상호 독립성을 유지하면서, 회귀분석에 사용될 수 있는 이론적 근거를 제시 (데이터 양이 충분해야 함)
- 서로 독립적이지 않은 데이터의 예 : 선수마다 보유하고 있는 네트워크
library(sand)
library(igraph)
g<-graph.formula(1-5, 1-7, 2-9, 2-4, 3-5, 4-5, 4-6, 4-7)
V(g)
E(g)
plot(g)
- 위 네트워크는 4번과 5번이 장악하고 있다.
- 새로운 멤버가 가입될때마다 변두리에 위치한 사람보다는 4번 / 5번처럼 관계망이 많은 사람과 연결되기 원하는 경향이 큼
- 결과적으로, 기존 연결 수치에 따라 새로운 연결고리가 만들어져 기존 다수의 연결망을 가진 사람에 더 많은 연결이 방생
- 새로운 데이터는 기존 데이터에 의존성을 가지게 됨
- 그러나 야구 데이터의 경우 홈런 20개를 기록한 타자가 21개를 기록할 때 20이 21에 주는 영향은 없으며 수치 간 완전 독립적임
데이터(관측자료)가 많다는 의미
- 평균값을 중심으로 관측자료의 빈도수가 균형 있게 작아지는 히스토그램을 만들 수 있음
a<-subset(Batting, yearID>2011&yearID<2016&AB>=300)
hist(a$H, main='949 players', breaks=seq(from=0, to=300, by=30))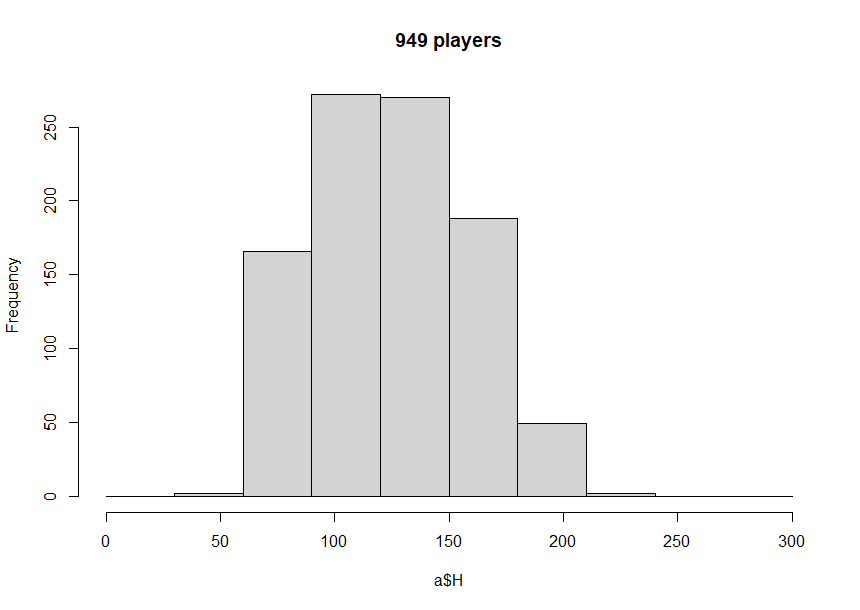
a<-subset(Batting,yearID>2011&yearID<2016&AB>=300&teamID=='NYA')
hist(a$H, main='32 players', breaks=seq(from=0, to=300, by=30))
회귀분석에서는 왜 정규분포 대신 스튜던트 t분포를 사용하는가?
- 정규분포와 t분포는 그 모양이 서로 닮았지만, 같지는 않음
curve(dnorm(x),-4,4,ylab='density')
curve(dt(x,df=3),add=TRUE,lty=2)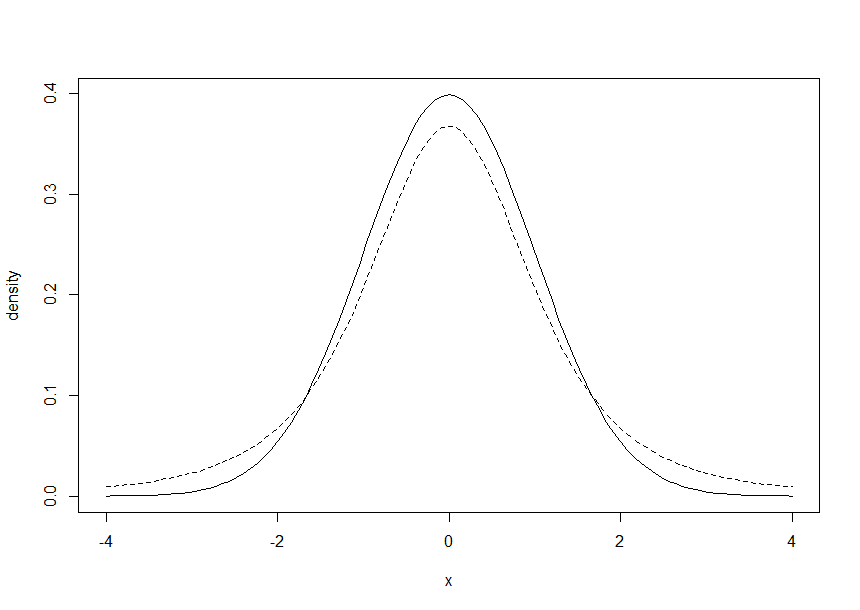
- 정규분포의 확률밀도가 더 높지만, 양쪽 꼬리부분의 밀도는 t분포가 더 높음
- 즉, 정규분포보다 t분포가 포함하는 예측범위가 더 넓다.
- 정규분포보다 표본의 수가 적을때 활용성이 더 높다. 표본의 수가 적을수록 경사는 더 완만해진다. (예측범위가 넓어진다.)
- 또한 정규분포보다 보수적인 통계분석이 가능해진다.
좋은 예측모델 구별법: 표준오차
- 회귀분석의 목적은 독립 변수를 이용해 알고 싶은 종속 변수를 예측하는 것이다.
- 예측을 위해 선행되어야 할 작업은 모델의 추론
- 예측방법은 추론에 대한 설명이 끝난 후에 점예측과 구간예측을 통해 설명
- 두 변수로 만든 산포도의 점들을 가장 잘 대변할 수 있는 선을 찾아내는 것이 좋은 예측모델의 기준

- 정규분포 가정에 부합하는 실제 관측점이 예측선에서 떨어진 정도가 가장 적을 때 회귀선이 결정됨
- 모델 추정에 사용된 알고리즘은 최소좌승법이라고 함
최소좌승법
- 좌승이란 종속 변수인 실제 승률과 회귀분석이 타율로 예측한 예상 승률 간 차이의 제곱
- 예측점에서 관측점이 벗어나 있는 잔차의 정도가 작을수록 신뢰성이 높은 모델이 됨
- 관측점마다 다른 크기의 잔차를 표준화한 표준오차(RMSE)가 작을수록 좋은 예측모델
선형회귀분석의 4대 가정
1. 선형성에 대한 가정
- 팀 타율 - 팀 승률의 관계처럼 우상향 곡선이 아닌, 나이 - 홈런 수와 같이 에이징 커브가 있는 비선형모델의 경우 선형회귀분석이 적절하지 않다.
- 이론적으로 선형이 맞더라도 실제 산포도가 곡선을 그리고 있다면, 로그함수 또는 지수함수를 이용해 선형으로 만든다.
- 로그함수를 이용해 변수 간 거리를 등차화해 곡선을 직선으로 만든다.
par(mfrow=c(1,2))
x<-c(1,2,4,8,16)
y<-c(1,2,3,4,5)
plot(x,y,type='b', lwd=3, main='Before Transformation')
x_adj<-log(x)
plot(x_adj,y,type='b', lwd=3, main='After Transformation')
2. 등분산성에 대한 가정
- 회귀선으로부터 관측된 모든 점이 동등한 분산을 두면서 분포되어 있어야 함
- 회귀선을 중심으로 어느 한쪽으로 치우쳐 있는 자료라면, 회귀분석에 적합하지 않음
- 잔차를 보여주는 적합성 그래프를 활용해 잔차의 불균형 여부, 불균형 여부의 이유를 확인할 수 있음
- 이상치 제거, 유연한 분석모델 채택 등의 해결방법이 있다.
- 유연한 분석모델을 채택하기 위해서는 이분산 여부를 알아보는 BPtest를 선행하고, 이분산이 발견됐다면 데이터 분산을 정규성에 가깝게 하는 Box-Cox 변형으로 개선가능하다.
library(Lahman)
rec<-subset(Teams, yearID==2014)
rec$wp<-rec$W/rec$G
a<-lm(wp~R, rec)
library(lmtest)
bptest(a)
>>>
studentized Breusch-Pagan test
data: a
BP = 3.5067, df = 1, p-value = 0.06112- 이분산이 없다는 귀무가설이 유의확률 0.06에 근거해 귀무가설이 사실이 아닐 가능성이 높은 것으로 나옴
- Box Cox 변형을 실시해서 이분산 가능성이 개선해본다
#box-cox 변형
library(caret)
b<-BoxCoxTrans(rec$wp)
c<-cbind(rec,wp_adj=predict(b, rec$wp))
d<-lm(wp_adj~R, c)
bptest(d)
>>>
studentized Breusch-Pagan test
data: d
BP = 3.3017, df = 1, p-value = 0.06921
3. 독립성에 대한 가정
- 개별 데이터 간에는 아무런 영향이 없어야 한다는 가정, 두 가지 의미를 가지고 있다.
- 독립변수는 종속 변수의 오류항과 아무런 연관성이 없어 결과적으로 종속 변수에서 독립되어야 함
- 종속 변수의 오류가 다른 종속 변수의 오류와 상관이 발생하지 않아야 함
4. 정규성에 대한 가정
- 의존 변수가 정규분포를 따르는지 확인
- 한쪽 쏠림현상(왜도)이 있어 분포의 꼬리가 지나치게 길진 않은지 확인
- 중심이 지나치게 높아 첨도현상이 발생하고 있는지 확인
- 대부분 최솟값 또는 최댓값이 지나치게 낮거나 높은 경우 쏠림현상이 발생
728x90
'Minding's Reading > 메이저리그 야구 통계학 2e' 카테고리의 다른 글
| [메이저리그 야구 통계학 2/e] 4장 - 상관관계는 인과관계가 아니다(2) (2) | 2023.05.08 |
|---|---|
| [메이저리그 야구 통계학 2/e] 4장 - 상관관계는 인과관계가 아니다(1) (0) | 2023.05.01 |
| [메이저리그 야구 통계학 2/e] 3장 - 선수의 능력은 어떻게 측정할 것인가?(2) (0) | 2023.04.25 |
| [메이저리그 야구 통계학 2/e] 3장 - 선수의 능력은 어떻게 측정할 것인가?(1) (0) | 2023.04.24 |
| [메이저리그 야구 통계학 2/e] 2장 - 메이저리그 데이터 마이닝 (2) | 2023.04.20 |