728x90
반응형
오늘은 로지스틱 회귀에 대해서 알아보았다.
로지스틱 회귀에 대한 자료와 정보는 아래 링크를 참고하였다.
6.1 로지스틱 회귀분석 — 데이터 사이언스 스쿨
.ipynb .pdf to have style consistency -->
datascienceschool.net
https://hleecaster.com/ml-logistic-regression-concept/
로지스틱회귀(Logistic Regression) 쉽게 이해하기 - 아무튼 워라밸
본 포스팅에서는 머신러닝에서 분류 모델로 사용되는 로지스틱 회귀 알고리즘에 대한 개념을 최대한 쉽게 소개한다. (이전에 선형회귀에 대한 개념을 알고 있다면 금방 이해할 수 있는 수준으
hleecaster.com
로지스틱 회귀 모델
- 결과 변수가 1 또는 0인 이진형 변수에서 쓰이는 회귀분석 방법 (분류문제에 쓰임)
- ex) 스팸메일일 확률이 0.5 이상이면 스팸메일로 분류하는 모델

로지스틱 회귀모델이 분류 문제에 쓰이는 이유

- 결과 변수가 이진형 변수일 경우 선형회귀는 이상치에 민감하기 때문에 이를 제대로 표현하지 못할 수 있음
- 또한, 예측값이 -∞ ~ ∞ 까지이므로 0 또는 1이 나올 확률을 계산하기 부적절함
- 로지스틱 회귀는 데이터가 특정 범주(0 또는 1)에 속할 확률을 예측하기 위해 다음과 같은 단계를 거침
- 모든 feature들의 계수(coefficient / 가중치)와 절편(intercept / bias)을 0으로 초기화
- 각 속성들의 값에 계수를 곱해서 log-odds를 구함
- log-odds를 sigmoid 함수에 넣어서 0 ~ 1 사이의 확률을 구함
Log-odds
- 선형회귀에서 각 속성에 값에 weight를 곱하고 bias를 더해서 예측값을 구하는 방식과 비슷
- 로지스틱 회귀에서는 예측값 대신 log-odds를 구해줌

- odds를 구하는 수식 : 사건이 발생할 확률을 사건이 발생하지 않을 확률로 나눈 값
- odds에 log를 취한 것이 log-odds (로그를 적용하면 odds가 정규분포를 따르게 되어 0~1 사이값으로 표현됨)
로지스틱 회귀에서의 log-odds 계산
- 로지스틱 회귀에서는 여러 feature들에 가중치(weight)를 곱하고 절편(bias)을 더해서 log-odds를 구해야 함
- 여러 속성들에 각각 가중치와 절편을 쉽게 적용하기 위해 dot product방식으로 log-odds를 구함
- 각 속성값이 포함된 행렬과 각각의 가중치가 포함된 행렬을 계산

- 연산은 numpy의 np.dot() 메서드를 통해 처리 가능
Sigmoid Function
- 로지스틱 회귀에서 확률은 0 ~ 1 사이의 커브 모양으로 나타내야 하는데, 이를 가능케 하는 것이 시그모이드 함수
- 위 수식으로 구한 log-odds를 sigmoid 함수에 넣어 0 ~ 1 사이의 값으로 변환시켜 줌
- e^(-z)는 지수함수이며, numpy의 np.exp(-z)로 구할 수 있음

Log Loss (로그 손실)
- 데이터를 잘 분류하는 적절한 가중치(weight)와 절편(bias)인지 판단하기 위해 손실(Loss) 고려
- 로지스틱회귀에 대한 손실함수는 Log Loss라고 하며, 다음과 같은 수식으로 구함

- 음의 로그함수를 사용하여 loss를 구함
- 음의 로그함수는 확률이 1일 때(100%일 때) loss로 0을 반환하고, 확률이 0에 가까워질수록 큰 값을 반환
- 즉, 정확한 예측일수록 낮은 값을 반환
- 경사하강법(Gradient Descent)을 사용하여 모든 데이터에서 log loss를 최소화하는 계수를 찾을 수 있음
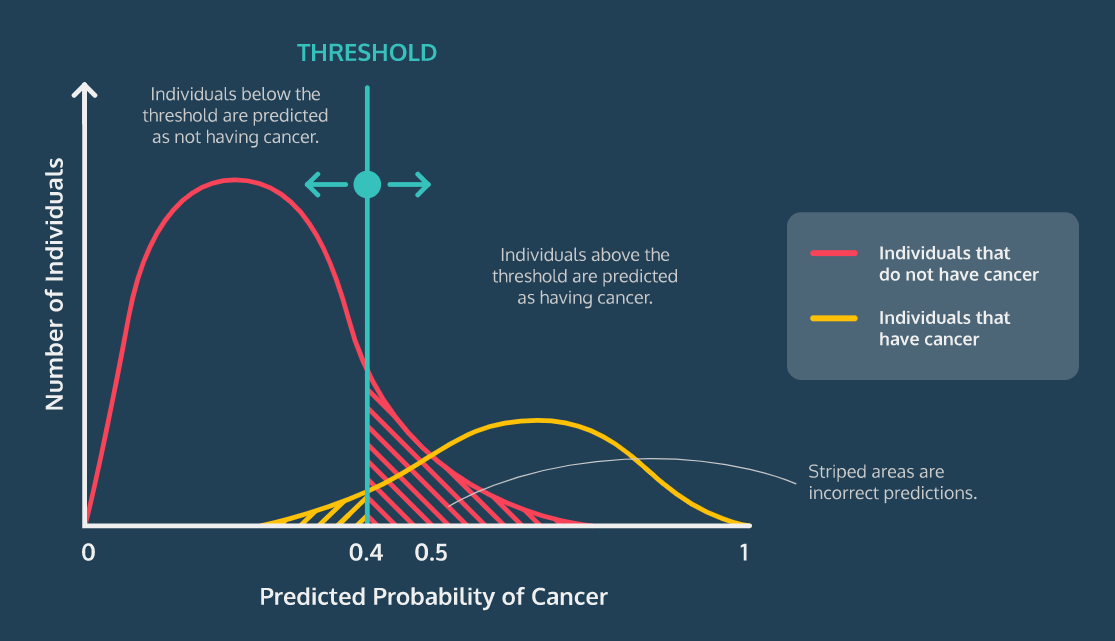
임계값(Classification Threshold)
- 기본 임계값은 0.5

- 분류모델에 따라 임계값을 변경 할 수 있음
- ex) 암 진단 모델의 경우 민감도를 높이기 위해 임계값을 낮춤
로지스틱 회귀 실습
- iris 데이터 이용
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris# iris 데이터 저장
iris = load_iris()
# iris 데이터의 target 값 (결과 값) 출력
print(iris.target_names)
>>>
['setosa' 'versicolor' 'virginica']# iris 데이터의 feature 종류
print(iris.feature_names)
>>>
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']# iris 데이터 값과 target값 (상위 5행)
print(iris.data[0:5])
print(iris.target[0:5]) # 0, 1, 2 각각 setosa, versicolor, virginica와 매핑
>>>
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
[0 0 0 0 0]# X는 iris 데이터, y는 타겟데이터
X = iris.data
y = iris.targetdf = pd.DataFrame(X, columns = ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'])
df.head()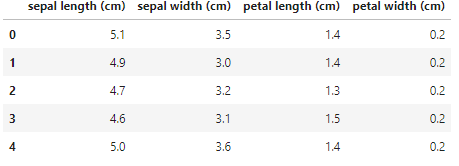
# DataFrame을 seaborn으로 시각화하기
vis = pd.DataFrame(iris.data, columns= iris.feature_names)
vis['species'] = np.array([iris.target_names[i] for i in iris.target])
# pairplot : 3차원 이상의 데이터에서 주로 사용
# hue : 카테고리형 데이터가 섞여있을 때, 이것을 기준으로 카테고리 값에 따라 색상을 달리 표시
sns.pairplot(vis, hue='species')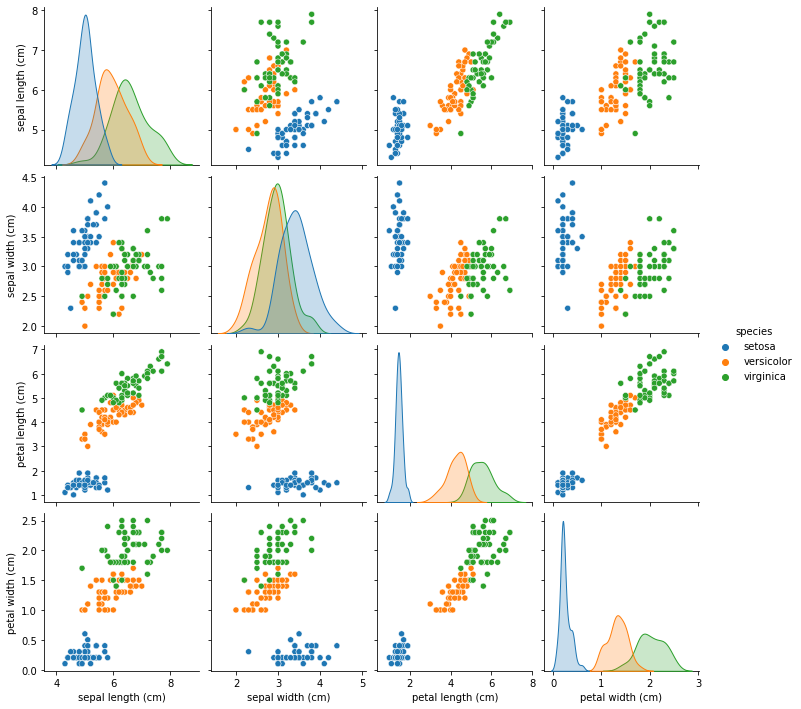
# train data와 test data로 나누기 (훈련7, 테스트3 비율)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)# 로지스틱 회귀모델 임포트 (scikit learn)
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()# 모델 피팅
log_reg.fit(X, y)# 가중치(Weight)와 편향(bias) 확인
W, b = log_reg.coef_, log_reg.intercept_
print(W, b)
>>>
[[-0.41943756 0.96749376 -2.5205723 -1.084326 ]
[ 0.53147635 -0.3150198 -0.20094963 -0.94785159]
[-0.11203879 -0.65247397 2.72152193 2.03217759]] [ 9.84186228 2.21913963 -12.06100191]# 정확도(score) 확인
print(log_reg.score(X_train, y_train))
>>>
0.9714285714285714# 로지스틱 회귀 모델로 X_test 데이터의 target을 예측한 결과
print(log_reg.predict(X_test))
>>>
[0 1 2 0 2 0 0 2 0 2 1 1 0 2 0 2 1 2 2 2 1 1 2 0 2 2 1 1 2 1 2 2 2 1 1 2 1
2 1 1 0 0 2 1 0]print(y_test)
>>>
[0 1 2 0 1 0 0 2 0 2 1 1 0 2 0 2 1 2 2 2 1 1 2 0 2 2 1 1 2 1 2 2 2 1 1 2 1
2 1 1 0 0 2 1 0]- 간단한 데이터 및 모델이라 전부 맞췄다
728x90
'Minding's Programming > Knowledge' 카테고리의 다른 글
| [ChatGPT] ChatGPT에게 여행일정을 짜달라고 해보았다. (0) | 2023.02.05 |
|---|---|
| [ML / DL] KNN (K-Nearest-Neighbor, K-최근접 이웃) (0) | 2022.01.25 |
| [ML/DL] 랜덤포레스트(Random Forest) & 앙상블(Ensemble) (0) | 2022.01.23 |
| [ML / DL] 의사결정나무 (Decision Tree) (0) | 2022.01.20 |
| [ML/DL] 선형회귀 (Linear Regression) (0) | 2022.01.18 |
