728x90
반응형
본인의 Github
https://github.com/JeongMinHyeok/Kalman_Filter
JeongMinHyeok/Kalman_Filter
Contribute to JeongMinHyeok/Kalman_Filter development by creating an account on GitHub.
github.com

추정과정
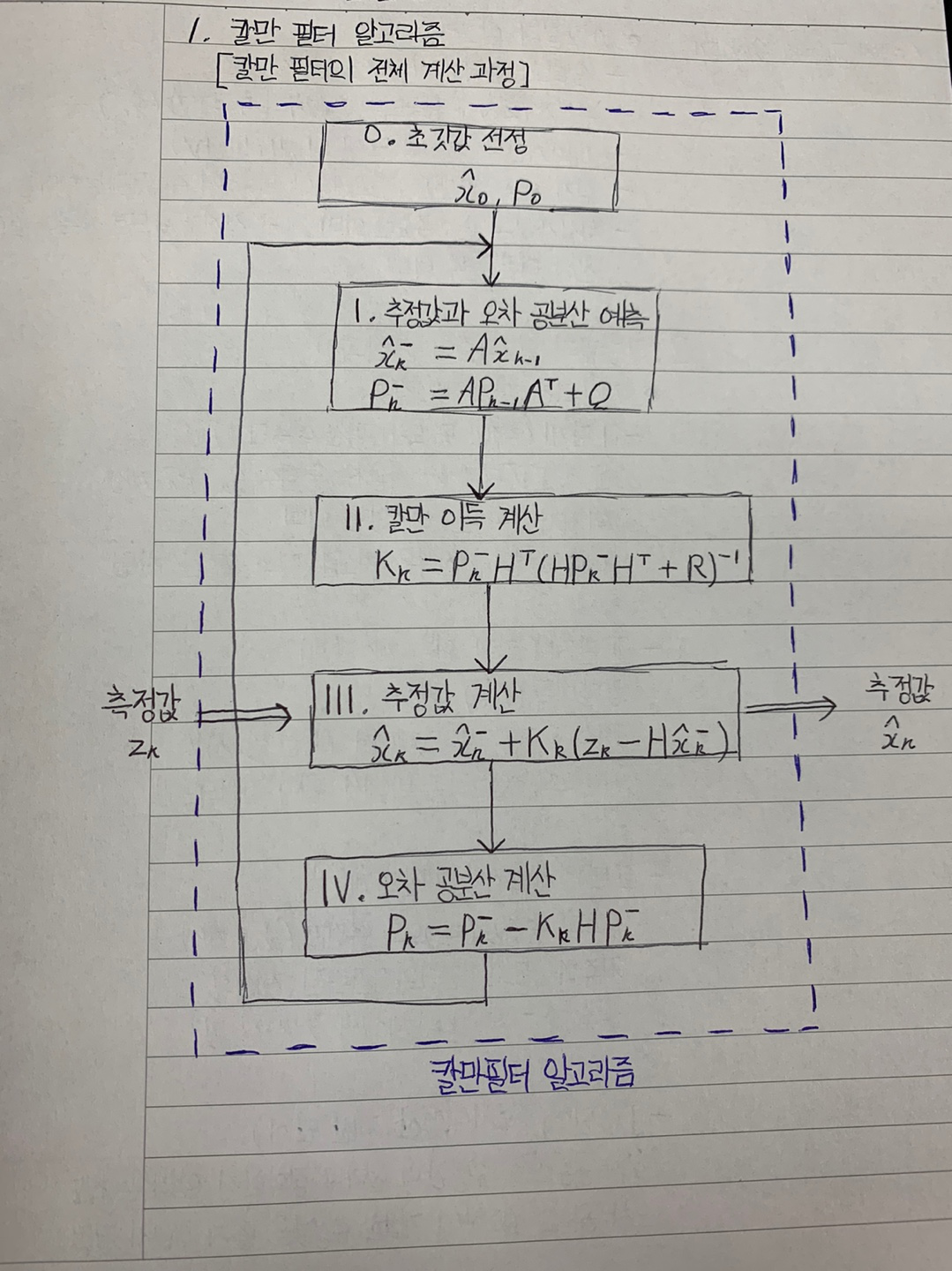
- 그림의 2 ~ 4단계에 해당
- 추정과정의 목표 : 칼만필터의 최종결과물인 추정값 계산 (3단계)
- 1차 저주파 통과 필터와 연결된 개념
추정값 계산 (3단계)
칼만필터 추정값 계산식과 1차 저주파 통과필터 계산식 비교 (식 전개)
- 1차 저주파 계산식 : x- k = (1-K)xk-1 + Kxk
- 칼만 필터 : x hat k = (I - Kk)x hat - k + Kkzk
칼만필터와 1차 저주파통과필터의 공통점
- 1차 저주파필터와 칼만필터는 각각 (직전추정값, 측정값)과 (예측값, 측정값)에 적절한 가중치를 곱한 다음, 두 값을 더해 최종 추정값 계산
변하는 가중치
- 칼만 필터의 추정값 계산과 1차 저주파 통과필터는 비슷하지만 완전히 똑같지는 않음
- H가 단위행렬이라고 가정했기 때문에 비슷한 형태를 가지게 된 것 (단위행렬이란?)
- 가정이 없더라도 계산방식이 비슷하다는 것은 유효함
칼만 필터만의 독특한 특징 (1차 저주파와 구별되는 점)
- 추정값 계산식을 통해 알아봄
- 예측값과 새로운 측정값이 있어야 함 (예측과정과 측정에서 값이 주어짐)
- H는 시스템 모델과 관련있는 행렬 (칼만필터 설계 전에 값이 주어짐)
- Kk는 칼만이득(Kalman gain), 칼만이득 계산식을 통해 값이 계산됨
- 1차 저주파에 사용하는 가중치(alpha)는 설계자가 임의로 선정하고 불변함
- 칼만필터는 알고리즘 반복하며 칼만이득 매번 다시 조정
오차 공분산 계산
- 추정값이 정확한지를 오차공분산을 통해 알 수 있음 (실제값과 차이 비교 = 추정오차)
- 이러한 이유로 추정값과 오차공분산 함께 출력하는 경우 종종 있음
실제값 (xk)과 추정값, 오차공분산 사이의 관계
- 변수 xk는 평균이 추정값(x hat k)이고, 공분산이 Pk인 정규분포를 따름
- 따라서 xk가 가질 수 있는 값의 확률은 위의 정규분포와 같음
- 정규분포 종 모양의 폭은 Pk가 결정
- 종 모양의 폭이 작으면 (Pk가 작으면) xk가 가질 수 있는 값이 평균(x hat k) 근처이므로 추정오차가 작음 (반대의 경우 추정오차 큼)

오차 공분산의 수학적 정의
- Pk = E{(xk - x hat k)(xk - x hat k)^T}
- E{}는 중괄호 안에 있는 변수의 평균 구하는 연산자
- xk는 참값, 우변의 xk - x hat k는 참값과 추정값의 차이 (추정오차)
- 즉, 오차공분산은 추정오차의 제곱을 평균한 값
5장 요약
- 칼만필터는 1차저주파 통과필터와 비슷한 방식으로 추정값 계산
- 1차 저주파 통과필터와 다른 점은 칼만이득(가중치)을 매번 새로 계산
- 추정값의 오차 공분산도 매번 계산, 이 값이 추정값의 정확도를 나타냄
728x90
'Minding's Reading > 칼만필터는 어렵지 않아' 카테고리의 다른 글
| [칼만필터는어렵지않아/Python] CH.07 시스템모델 (0) | 2021.06.24 |
|---|---|
| [칼만필터는 어렵지않아/Python] CH.06 예측과정 (0) | 2021.06.24 |
| [칼만필터는어렵지않아/Python] CH.04 칼만필터 (2) | 2021.06.22 |
| [칼만필터는 어렵지않아 / Python] CH.03 저주파 통과 필터 (0) | 2021.06.21 |
| [칼만필터는 어렵지 않아/Python] CH.02 이동평균 필터 (0) | 2021.06.19 |