728x90
반응형
tbmoon님의 Github (칼만필터는 어렵지 않아 Python 구현)
https://github.com/tbmoon/kalman_filter
tbmoon/kalman_filter
Kalman Filter in Python (파이썬으로 구현하는 칼만 필터). Contribute to tbmoon/kalman_filter development by creating an account on GitHub.
github.com
본인의 Github (공부내용 간단정리)
https://github.com/JeongMinHyeok/Kalman_Filter
JeongMinHyeok/Kalman_Filter
Contribute to JeongMinHyeok/Kalman_Filter development by creating an account on GitHub.
github.com

저주파 통과 필터 (low-pass filter)
이동평균의 한계
- 이동평균필터의 정의 별도의 항으로 풀어쓰기
- 모든데이터에 동일가중치 부여함
- 최신 측정값(데이터)이 현재값과 비슷할 가능성이 높으나, 오래된 데이터와 동일 가중치 처리
- 이동평균필터를 사용할 때는 장점과 한계 정확히 알고 적재적소 적용하는 것이 중요
1차 저주파 통과 필터
- 최근 측정값에는 높은 가중치, 오래된 값에는 낮은 가중치를 주는 필터
- 재귀식 (책의 식 3.1)
- alpha는 0 < alpha < 1인 임의의 상수
- 저주파통과필터의 x hat k는 평균과 관련없음, '추정값'이라는 용어로 사용
- 더 오래된 값에 더 낮은 가중치 부여함
- 측정데이터에 곱해진 계수 a(1-a)와 1-a 크기 비교
- alpha가 0 < a < 1인 상수이므로,
- a(1-a) < 1-a (a가 곱해질수록 작아지기 때문)
- 1차 저주파 통과필터는 지수가중(exponentially weighted)필터라고도 부름
저주파 통과 필터 함수
- 예제(2장과 동일) : 이평손 연구원은 초음파 거리계는 개발하는 중이다. 시제품의 성능을 검증하기 위해 헬기에 초음파거리계를 장착하고 지면까지의 거리를 측정하는 비행 시험을 실시했다. 측정값은 0.02초 간격으로 저장했다. 그런데 헬기의 진동, 지면 상태 등의 영향으로 측정 데이터에 잡음이 심했다. 이동평균필터로 이 잡음을 제거해보자.
import numpy as np
import matplotlib.pyplot as plt
from scipy import io
# 초음파 측정 데이터
input_mat = io.loadmat('./data/3.LPF/SonarAlt.mat')def low_pass_filter(x_meas, x_esti):
"""저주파 통과 필터 함수를 통해 초음파 계산"""
x_esti = alpha * x_esti + (1 - alpha) * x_meas
return x_esti
def get_sonar(i):
"""초음파 측정값 반환"""
z = input_mat['sonarAlt'][0][i] # input_mat['sonaralt']: (1, 1501)
return z# Input parameters.
alpha = 0.7
n_samples = 500
time_end = 10
dt = time_end / n_samples
time = np.arange(0, time_end, dt)
x_meas_save = np.zeros(n_samples)
x_esti_save = np.zeros(n_samples)x_esti = None
for i in range(n_samples):
x_meas = get_sonar(i)
if i == 0:
x_esti = x_meas
else:
x_esti = low_pass_filter(x_meas, x_esti)
x_meas_save[i] = x_meas
x_esti_save[i] = x_estiplt.plot(time, x_meas_save, 'r*', label='Measured')
plt.plot(time, x_esti_save, 'b-', label='Low-pass Filter')
plt.legend(loc='upper left')
plt.title('Measured Altitudes v.s. LPF Values')
plt.xlabel('Time [sec]')
plt.ylabel('Altitude [m]')
plt.show()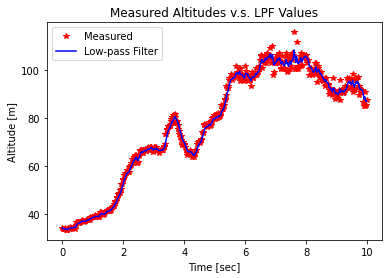
- 측정데이터의 잡음 제거 및 고도 변화 추이 잘 나타나 있음
- 측정데이터에 맞게 alpha 선정했는지가 중요
alpha값을 다르게 설정했을 때 (0.4 / 0.9)
# alpha를 0.4로 설정
alpha = 0.4
n_samples = 500
time_end = 10
dt = time_end / n_samples
time = np.arange(0, time_end, dt)
low_x_meas_save = np.zeros(n_samples)
low_x_esti_save = np.zeros(n_samples)
x_esti = None
for i in range(n_samples):
x_meas = get_sonar(i)
if i == 0:
x_esti = x_meas
else:
x_esti = low_pass_filter(x_meas, x_esti)
low_x_meas_save[i] = x_meas
low_x_esti_save[i] = x_esti# alpha를 0.9로 설정
alpha = 0.9
dt = time_end / n_samples
time = np.arange(0, time_end, dt)
high_x_meas_save = np.zeros(n_samples)
high_x_esti_save = np.zeros(n_samples)
x_esti = None
for i in range(n_samples):
x_meas = get_sonar(i)
if i == 0:
x_esti = x_meas
else:
x_esti = low_pass_filter(x_meas, x_esti)
high_x_meas_save[i] = x_meas
high_x_esti_save[i] = x_estiplt.plot(time, low_x_esti_save, 'r-', label='alpha=0.4')
plt.plot(time, high_x_esti_save, 'b-', label='alpha=0.9')
plt.legend(loc='upper left')
plt.title('Measured Altitudes v.s. LPF Values')
plt.xlabel('Time [sec]')
plt.ylabel('Altitude [m]')
plt.show()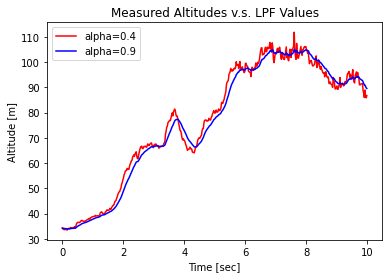
- alpha가 작으면 잡음이 더 많고, alpha가 크면 잡음은 줄지만 시간지연이 커짐
- alpha가 작으면 1-alpha값이 상대적으로 더 커져 측정값의 변화에 더 민감
- alpha가 크면 직전 추정값의 비중이 더 커져 그래프의 변화 무뎌짐
3장 요약
- 1차 저주파 통과 필터의 수식은 간단하고 구현하기 쉬움
- 이동평균 필터와 달리 최신 측정값에 더 큰 가중치
- 이동평균 필터보다 측정 신호의 변화 추이를 더 잘 감지
- 1차 저주파 통과 필터와 지수 가중 이동평균필터는 같은 필터를 뜻함
728x90
'Minding's Reading > 칼만필터는 어렵지 않아' 카테고리의 다른 글
| [칼만필터는 어렵지않아/Python] CH.06 예측과정 (0) | 2021.06.24 |
|---|---|
| [칼만필터는 어렵지않아 / Python] CH.05 추정과정 (0) | 2021.06.23 |
| [칼만필터는어렵지않아/Python] CH.04 칼만필터 (2) | 2021.06.22 |
| [칼만필터는 어렵지 않아/Python] CH.02 이동평균 필터 (0) | 2021.06.19 |
| [칼만필터는 어렵지 않아] CH.01 평균필터 (2) | 2021.06.16 |