728x90
반응형
Python 코드 원본 tbmoon님의 Github:
https://github.com/tbmoon/kalman_filter
tbmoon/kalman_filter
Kalman Filter in Python (파이썬으로 구현하는 칼만 필터). Contribute to tbmoon/kalman_filter development by creating an account on GitHub.
github.com
본인의 Github (칼만필터 공부 정리)
https://github.com/JeongMinHyeok/Kalman_Filter
JeongMinHyeok/Kalman_Filter
Contribute to JeongMinHyeok/Kalman_Filter development by creating an account on GitHub.
github.com

영상 속의 물체 추적하기
- 표적의 위치는 영상 처리 알고리즘(Object Detection 등)으로 알아내야 함
- 칼만필터는 획득한 추정값에 오차를 제거하고, 이동속도를 추정하는 역할
시스템 모델
상태변수 정의
- 평면 상의 표적 추적에 칼만필터를 적용하기 위해 앞 장의 위치-속도 모델을 2차원으로 확장
- 상태변수를 가로방향(x축)의 위치와 속도, 세로방향(y축)의 위치와 속도로 설정하고 시스템 모델 유도
- 상태변수의 위치는 중요하지 않음 : (위치x, 위치y, 속도x, 속도y) 이렇게 설정해도 상관없음
상태변수 정의에 따른 시스템 모델
- xk+1 = Axk + wk
- zk = Hxk + vk
- 시스템 모델은 위치와 속도 사이의 관계를 2차원 평면으로 확장한 것
- 대상 표적의 위치는 영상처리 알고리즘으로 찾아 칼만필터에 입력, 속도는 측정하지 않음
칼만필터함수
- 공 이미지를 추적하는 예제
import numpy as np
import matplotlib.pyplot as plt
import cv2
from numpy.linalg import inv
from skimage.metrics import structural_similarity
np.random.seed(0)def kalman_filter(z_meas, x_esti, P):
"""칼만필터 알고리즘 (매개변수 : 측정값, 추정값, 오차공분산)"""
# (1) Prediction.
x_pred = A @ x_esti
P_pred = A @ P @ A.T + Q
# (2) Kalman Gain.
K = P_pred @ H.T @ inv(H @ P_pred @ H.T + R)
# (3) Estimation.
x_esti = x_pred + K @ (z_meas - H @ x_pred)
# (4) Error Covariance.
P = P_pred - K @ H @ P_pred
return x_esti, P- get_ball_pos 함수 : 공의 위치를 찾아내는 알고리즘
def get_ball_pos(iimg=0):
"""Return measured position of ball by comparing with background image file.
- References:
(1) Data Science School:
https://datascienceschool.net/view-notebook/f9f8983941254a34bf0fee42c66c5539
(2) Image Diff Calculation:
https://www.pyimagesearch.com/2017/06/19/image-difference-with-opencv-and-python
"""
# Read images.
imageA = cv2.imread('./data/10.TrackKalman/Img/bg.jpg')
imageB = cv2.imread('./data/10.TrackKalman/Img/{}.jpg'.format(iimg+1))
# Convert the images to grayscale.
grayA = cv2.cvtColor(imageA, cv2.COLOR_BGR2GRAY)
grayB = cv2.cvtColor(imageB, cv2.COLOR_BGR2GRAY)
# 두 이미지 사이의 구조적 유사성 지수(SSIM) 계산, 차이 이미지가 반환되는지 확인.
_, diff = structural_similarity(grayA, grayB, full=True)
diff = (diff * 255).astype('uint8')
# 서로 다른 두 이미지(배경, 공)의 영역을 구하기 위해 이미지 임계값 지정 후 윤곽선 찾기
thresh = cv2.threshold(diff, 0, 255, cv2.THRESH_BINARY_INV | cv2.THRESH_OTSU)[1]
contours, _ = cv2.findContours(thresh.copy(), cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
M = cv2.moments(contours[0])
xc = int(M['m10'] / M['m00']) # center of x as true position.
yc = int(M['m01'] / M['m00']) # center of y as true position.
v = np.random.normal(0, 15) # v: 위치의 측정잡음
xpos_meas = xc + v # x_pos_meas: 위치x의 측정값 (observable).
ypos_meas = yc + v # y_pos_meas: 위치y의 측정값 (observable).
return np.array([xpos_meas, ypos_meas])# Input parameters.
n_samples = 24
dt = 1
# Initialization for system model.
# Matrix: A, H, Q, R, P_0
# Vector: x_0
A = np.array([[ 1, dt, 0, 0],
[ 0, 1, 0, 0],
[ 0, 0, 1, dt],
[ 0, 0, 0, 1]])
H = np.array([[ 1, 0, 0, 0],
[ 0, 0, 1, 0]])
Q = 1.0 * np.eye(4)
R = np.array([[50, 0],
[ 0, 50]])
# Initialization for estimation.
x_0 = np.array([0, 0, 0, 0]) # (x-pos, x-vel, y-pos, y-vel) by definition in book. / 추정값 초기위치
P_0 = 100 * np.eye(4)
xpos_meas_save = np.zeros(n_samples)
ypos_meas_save = np.zeros(n_samples)
xpos_esti_save = np.zeros(n_samples)
ypos_esti_save = np.zeros(n_samples)# 칼만필터 실행
x_esti, P = None, None
for i in range(n_samples):
z_meas = get_ball_pos(i)
if i == 0:
x_esti, P = x_0, P_0
else:
x_esti, P = kalman_filter(z_meas, x_esti, P)
xpos_meas_save[i] = z_meas[0]
ypos_meas_save[i] = z_meas[1]
xpos_esti_save[i] = x_esti[0]
ypos_esti_save[i] = x_esti[2]추적 결과
fig = plt.figure(figsize=(8, 8))
plt.gca().invert_yaxis()
plt.scatter(xpos_meas_save, ypos_meas_save, s=300, c="r", marker='*', label='Position: Measurements')
plt.scatter(xpos_esti_save, ypos_esti_save, s=120, c="b", marker='o', label='Position: Estimation (KF)')
plt.legend(loc='lower right')
plt.title('Position: Meas. v.s. Esti. (KF)')
plt.xlabel('X-pos. [m]')
plt.ylabel('Y-pos. [m]')
plt.xlim((-10, 350))
plt.ylim((250, -10))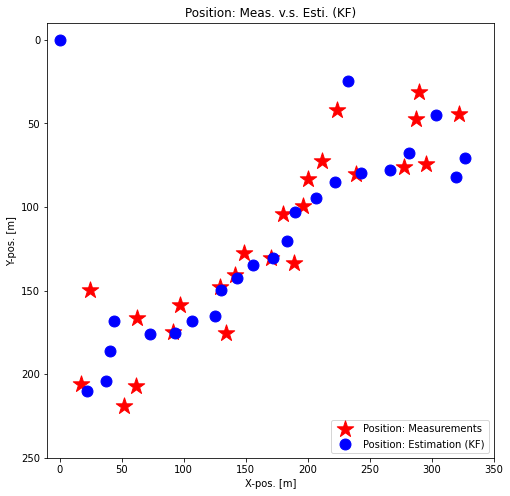
- 칼만필터의 추정위치가 측정값보다 대각선에 더 가깝게 위치함 (공은 실제로 대각선 움직임)
- 추정값의 초기위치가 (0,0)으로 설정되어 있어 초기 오차 큰 모습보임
plt.ion()
for i in range(n_samples):
fig = plt.figure(figsize=(8, 8))
image = cv2.imread('./data/10.TrackKalman/Img/{}.jpg'.format(i+1))
imgplot = plt.imshow(image)
plt.scatter(xpos_meas_save[i], ypos_meas_save[i], s=300, c="r", marker='*', label='Position: Measurements')
plt.scatter(xpos_esti_save[i], ypos_esti_save[i], s=120, c="b", marker='o', label='Position: Estimation (KF)')
plt.legend(loc='lower right')
plt.title('Position: True v.s. Meas. v.s. Esti. (KF)')
plt.xlabel('X-pos. [m]')
plt.ylabel('Y-pos. [m]')
plt.xlim((-10, 350))
plt.ylim((250, -10))
fig.canvas.draw()
plt.show()
plt.pause(0.05)
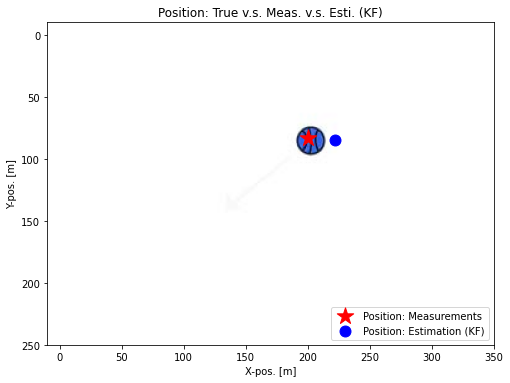
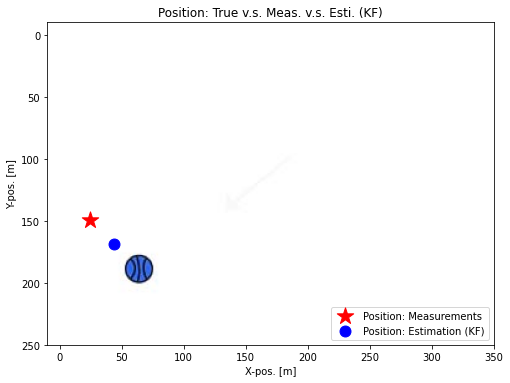

- 별표시 : 측정값 / 동그라미 : 추정값
- 실제 공의 위치와 측정값, 추정값의 차이 알 수 있음
- 측정값은 잡음의 영향 많이 받으며, 추정값은 이에 비해 매끄러운 궤도 보임
행렬 Q와 R 조율하여 성능 개선하기
- 행렬 Q의 크기가 커지면, 칼만이득이 커져 추정결과가 측정값에 더 가까워짐
- 행렬 Q의 크기가 작아지면, 칼만이득이 작아져 추정결과가 이전추정값과 비슷해짐 (더 매끄러운 궤적)
- 행렬 R은 행렬Q와 반대의 영향을 줌
728x90
'Minding's Reading > 칼만필터는 어렵지 않아' 카테고리의 다른 글
| [칼만필터는 어렵지않아/Python] CH.13 무향 칼만 필터 (0) | 2021.07.06 |
|---|---|
| [칼만필터는 어렵지않아/Python] CH.12 확장 칼만 필터 (0) | 2021.07.05 |
| [칼만필터는어렵지않아/Python] CH.09 위치로 속도 추정하기 (1) | 2021.06.30 |
| [칼만필터는어렵지않아/Python] CH.07 시스템모델 (0) | 2021.06.24 |
| [칼만필터는 어렵지않아/Python] CH.06 예측과정 (0) | 2021.06.24 |