큐 (Queues)
큐 또한 스택과 함께 많이 사용되는 자료 구조이다. 스택과 마찬가지로 선형 구조라는 공통점을 가지고 있지만, 다른 특성을 가지고 있다. 스택이 LIFO(후입선출) 방식인 반면에, 큐는 FIFO(선입선출) 방식을 가지고 있다.
데이터 원소를 큐에 넣는 동작을 인큐 (enqueue) 연산이라고 부르고, 반대로 큐로부터 데이터 원소를 꺼내는 동작을 디큐 (dequeue) 연산이라고 부른다.
큐를 구현할 때는 선형 배열(리스트)보다 연결 리스트를 사용하는 것이 더 유리하다. 선형 배열은 디큐 연산 시 모든 원소를 한 칸씩 옮겨야 하기 때문에, 시간 복잡도 측면에서 불리하기 때문이다.
양방향 연결 리스트를 이용한 큐 구현
class Node:
def __init__(self, item):
self.data = item
self.prev = None
self.next = None
class DoublyLinkedList:
def __init__(self):
self.nodeCount = 0
self.head = Node(None)
self.tail = Node(None)
self.head.prev = None
self.head.next = self.tail
self.tail.prev = self.head
self.tail.next = None
def __repr__(self):
if self.nodeCount == 0:
return 'LinkedList: empty'
s = ''
curr = self.head
while curr.next.next:
curr = curr.next
s += repr(curr.data)
if curr.next.next is not None:
s += ' -> '
return s
def getLength(self):
return self.nodeCount
def traverse(self):
result = []
curr = self.head
while curr.next.next:
curr = curr.next
result.append(curr.data)
return result
def reverse(self):
result = []
curr = self.tail
while curr.prev.prev:
curr = curr.prev
result.append(curr.data)
return result
def getAt(self, pos):
if pos < 0 or pos > self.nodeCount:
return None
if pos > self.nodeCount // 2:
i = 0
curr = self.tail
while i < self.nodeCount - pos + 1:
curr = curr.prev
i += 1
else:
i = 0
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def insertAfter(self, prev, newNode):
next = prev.next
newNode.prev = prev
newNode.next = next
prev.next = newNode
next.prev = newNode
self.nodeCount += 1
return True
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
prev = self.getAt(pos - 1)
return self.insertAfter(prev, newNode)
def popAfter(self, prev):
curr = prev.next
next = curr.next
prev.next = next
next.prev = prev
self.nodeCount -= 1
return curr.data
def popAt(self, pos):
if pos < 1 or pos > self.nodeCount:
raise IndexError('Index out of range')
prev = self.getAt(pos - 1)
return self.popAfter(prev)
def concat(self, L):
self.tail.prev.next = L.head.next
L.head.next.prev = self.tail.prev
self.tail = L.tail
self.nodeCount += L.nodeCount
class LinkedListQueue:
def __init__(self):
self.data = DoublyLinkedList() # self가 아닌 self.data가 리스트인 것 유의
def size(self):
return self.data.getLength()
def isEmpty(self):
return self.size() == 0
def enqueue(self, item):
node = Node(item)
self.data.insertAt(self.size()+1,node)
def dequeue(self):
return self.data.popAt(1)
def peek(self):
return self.data.head.next.data
환형(원형) 큐 (Circular Queues)
컴퓨터 시스템에서 큐는 많은 곳에서 이용된다. 프린터 대기열, 네트워크의 패킷 등 운영체제 내에서도 많이 쓰인다. (자료 생성과 자료 이용 작업이 비동기적으로 일어나는 경우)
큐에 담을 수 있는 데이터의 양이 무한하지는 않을 것이다. 큐의 길이를 한정하고 이를 잘 지킬 수 있을 때 큐를 효과적으로 사용할 수 있다. 큐의 맨 앞과 맨 뒤가 맞닿아 있다고 생각하고, 해당 위치를 기억한다면, 데이터 원소가 빠져나간 쪽의 저장소를 재활용하면서 큐를 관리할 수 있다. 이러한 모습의 큐가 환형 큐라고 한다.
코드 구현
class CircularQueue:
def __init__(self, n):
self.maxCount = n
self.data = [None] * n
self.count = 0
self.front = -1
self.rear = -1
def size(self):
return self.count
def isEmpty(self):
return self.count == 0
def isFull(self): # 최대 길이가 정해져 있으므로 함수 추가
return self.count == self.maxCount
def enqueue(self, x):
if self.isFull():
raise IndexError('Queue full')
self.rear = (self.rear + 1) % self.maxCount # 최대 길이에 도달할 경우 0으로 되돌아가도록
self.data[self.rear] = x
self.count += 1
def dequeue(self):
if self.isEmpty():
raise IndexError('Queue empty')
self.front = (self.front + 1) % self.maxCount # 최대 길이에 도달할 경우 0으로 되돌아가도록
x = self.data[self.front]
self.count -= 1
return x
def peek(self):
if self.isEmpty():
raise IndexError('Queue empty')
return self.data[(self.front + 1) % self.maxCount] # dequeue 실행 시 나오게 되는 원소 peek
우선 순위 큐 (Priority Queues)
우선순위 큐는 큐가 FIFO 방식을 따르지 않고 원소들의 우선순위에 따라 큐에서 빠져나오는 방식의 큐를 말한다.
우선순위 큐를 구현하는 방식은 크게 두 가지가 있다.
- Enqueue할 때 우선순위 순서를 유지하도록 설정
- Dequeue 할 때 우선순위가 가장 높은 것을 선택하는 방법
이 두 가지 방법에서는 Enqueue할 때 우선순위 순서를 유지하도록 설정하는 것이 유리하다. Dequeue할 때 선택을 한다면, 모든 원소들을 들여다 보아야 하기 때문이다.
우선 순위 큐 구현 (양방향 연결 리스트 이용)
class PriorityQueue:
def __init__(self):
self.queue = DoublyLinkedList()
def size(self):
return self.queue.getLength()
def isEmpty(self):
return self.size() == 0
def enqueue(self, x):
newNode = Node(x)
curr = self.queue.head # 첫 번째 노드(head)를 가리킴
while curr.next != self.queue.tail and x < curr.next.data: # tail 직전까지 우선 순위에 맞는 위치 찾음
curr = curr.next
self.queue.insertAfter(curr, newNode)
def dequeue(self):
return self.queue.popAt(self.queue.getLength())
def peek(self):
return self.queue.getAt(self.queue.getLength()).data위 코드는 수가 작을수록 우선 순위가 높아진다. 숫자가 작아질수록 dequeue가 실행되는 위치인 뒤쪽으로 간다.
* while 반복문에서 and 조건을 사용할 때 각 조건의 순서에 유의하자. and 조건 중 앞 조건이 맞지 않을 경우 뒷 조건은 무시하는데, x < curr.next.data 조건의 경우 curr.next가 tail이거나 None일 경우 에러가 발생한다.
트리(Trees)
트리는 뿌리(root)노드부터 시작해 간선(edge)들이 가지를 뻗어나가듯이 가지치기된 자료 구조를 뜻한다. 그림으로 표시할 때는 뿌리노드가 맨 위로 오기 때문에 나무를 뒤집어 놓은 듯한 모습이 된다.
트리에 쓰이는 용어 정리
- 노드 (nodes): 데이터가 들어있는 정점
- 간선 (edges): 노드들을 이어주는 선
- 루트 노드 (root node): 트리의 시작점(노드)
- 리프 노드 (leaf nodes): 트리의 끝 점(노드)
- 내부 노드 (internal nodes): 루트노드와 리프노드 사이에 있는 노드들
- 부모 (parent) 노드와 자식 (child) 노드: 가지가 뻗어난 노드 중 위에 있는 노드가 부모, 아래가 자식노드
- 형제 (sibling) 노드: 같은 부모 노드를 가진 노드들
- 노드의 수준 (level): 루트 노드의 레벨 0부터 가지가 자식 노드를 생성할 때마다 수준(level)이 1씩 오름.
- 노드의 차수 (degree): 자식(서브트리)의 수
- 트리의 높이 (height) - 또는, 깊이 (depth) - : 최대 수준(level) +1
- 부분 트리 (서브트리; subtrees): 특정 내부 노드를 루트 노드로 삼아 아래 후손 노드를 떼어낸 트리
- 이진 트리 (binary trees): 빈 트리이거나, 모든 노드의 차수가 2 이하인 트리
- 포화 이진 트리 (full binary trees): 모든 레벨에서 노드들이 채워져 있는 이진 트리 (높이가 k이고 노드개수가 2^k - 1)
- 완전 이진 트리 (complete binary trees): k-2까지는 포화 이진 트리이며, k-1레벨의 경우 제일 왼쪽부터 차례대로 채워져 있는 트리(k-1 레벨에는 차례만 중요하고 모두 채워져있지 않아도 됨)
이진 트리 코드 구현
트리 노드 생성자 코드
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None위 코드를 이용해 아래와 같은 연산을 생각해볼 수 있다.
- size() - 현재 트리에 포함되어 있는 노드의 수를 구함
- depth() - 현재 트리의 깊이 (또는 높이)를 구함
트리 자체의 정의가 재귀적이기 때문에, 트리 대상 연산 또한 대부분 재귀적으로 구현 가능하다. size()의 경우 루트 노드를 기준으로 양 옆으로 펼쳐진 서브트리의 size()를 구하는 방식으로 뻗어나가면 이진 트리 전체의 size를 구할 수 있다. (left tree + right tree + 1(자기 자신))
class Node:
def size(self):
l = self.left.size() if self.left else 0
r = self.right.size() if self.right else 0
return l+r+1
class BinaryTree:
# 빈 트리일 경우 대비
def size(self):
if self.root:
return self.root.size()
else:
return 0
depth() 연산자 또한 각 서브트리 별로 depth()를 구한 다음, 서브 트리의 depth()가 더 큰 서브 트리에 1을 더해주면 해당 이진 트리의 depth를 구할 수 있다.
(코드)
트리의 순회 - 깊이 우선 순회
트리를 순회하는 방법은 크게 두 가지가 있는데, 우선 두 가지 중 깊이 우선 순회에 대해 알아본다.
이진 트리를 대상으로 하는 깊이 우선 순회 방법에는 아래와 같은 3가지의 서로 다른 순서를 정의할 수 있다.
- 중위 순회 (in-order traverasl): 왼쪽 서브트리를 순회한 뒤 노드 x 를 방문, 그리고 나서 오른쪽 서브트리를 순회
- 전위 순회 (pre-order traversal): 노드 x 를 방문한 후에 왼쪽 서브트리를 순회, 마지막으로 오른쪽 서브트리를 순회
- 후위 순회 (post-order traversal): 왼쪽 서브트리를 순회, 오른쪽 서브트리를 순회, 그리고 나서 마지막으로 노드 x 를 방문
중위 순회 코드 구현
class Node: # 노드의 메서드로 구현
def inorder(self):
traversal = [] # 데이터를 반환할 리스트
if self.left:
traversal += self.left.inorder()
traversal.append(self.data)
if self.right:
traversal += self.right.inorder()
return traversal
class BinaryTree: # 이진 트리에 적용할 때
def inorder(self):
if self.root: # 빈 트리가 아닌 경우
return self.root.inorder()
else:
return []
전위 순회 / 후위 순회 코드 구현
class Node:
# 전위 순회
def preorder(self):
traversal = []
traversal.append(self.data)
if self.left:
traversal += self.left.preorder()
if self.right:
traversal += self.right.preorder()
return traversal
# 후위 순회
def postorder(self):
traversal = []
if self.right:
traversal += self.right.postorder()
traversal.append(self.data)
if self.left:
traversal += self.left.postorder()
return traversal중위 순회 코드의 순서만 바꿔주면 된다. class BinaryTree에서의 코드 구현도 거의 비슷해 이 글엔 적지 않았다.
트리의 순회 - 넓이 우선 순회
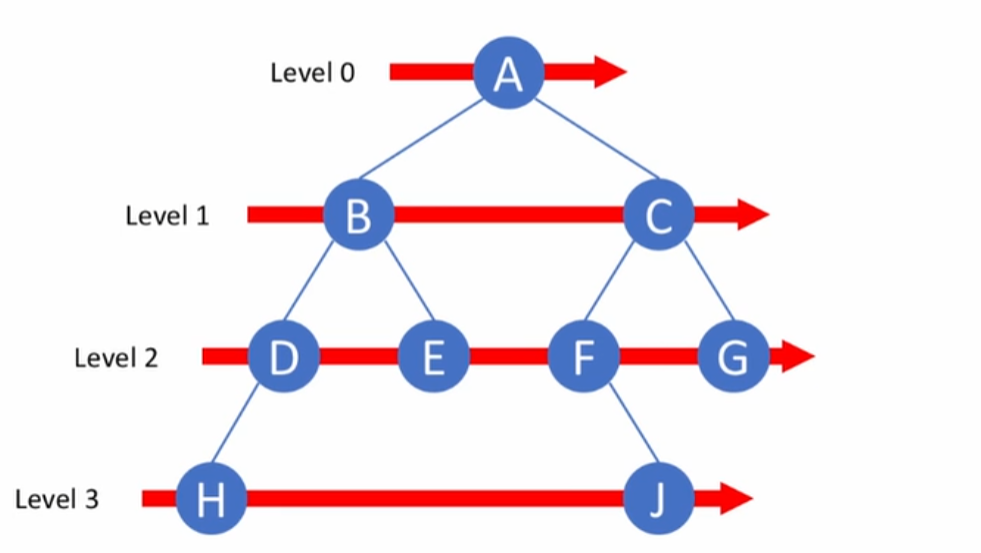
트리를 순회하는 방법에는 넓이 우선 순회라는 2번째 방법도 있다. 이 방법은 노드의 수준(level) 별로 순서를 정해 노드들을 방문하는 순회 방식이다. 수준이 낮은 노드를 우선으로 방문하며, 같은 수준의 노드들 사이에서는 부모 노드의 방문 순서에 따라 방문한다.(왼쪽부터 방문)
이 방식은 재귀적으로 구성되는 것이 아닌, 하나의 노드를 방문했을 때 나중에 그 노드의 자식 노드들을 방문하기로 하고 그 순서를 기억해두는 방식으로 진행한다. 이 방식에 가장 좋은 자료 구조는 큐(queue)이다. 선입선출(FIFO)의 구조를 가지고 있기 때문이다.
넓이 우선 순회 코드 구현
class ArrayQueue:
def __init__(self):
self.data = []
def size(self):
return len(self.data)
def isEmpty(self):
return self.size() == 0
def enqueue(self, item):
self.data.append(item)
def dequeue(self):
return self.data.pop(0)
def peek(self):
return self.data[0]
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None
class BinaryTree:
def __init__(self, r):
self.root = r
def bft(self):
if self.root:
traversal = []
q = ArrayQueue()
q.enqueue(self.root)
while q.isEmpty() == False: # queue가 비어있지 않을 때
node = q.dequeue()
traversal.append(node.data) # queue에 있던 노드의 데이터 리스트에 추가
if node.left: # 왼쪽 노드 queue에 추가
q.enqueue(node.left)
if node.right: # 오른쪽 노드 queue에 추가
q.enqueue(node.right)
return traversal
else: # 빈 트리일 경우 빈 리스트 반환
return []
이진 탐색 트리(Binary Search Tree)
이진 탐색 트리는 이진 트리의 일종이다. 이진 탐색과 똑같은 알고리즘은 아니지만, 많이 닮아 있는 면이 있다.
이진 탐색 트리도 마찬가지로 '이미 정렬된 트리'가 필요하다. 이진 탐색 트리는 현재 노드를 기준으로 왼쪽은 작은 값, 오른 쪽은 큰 값을 가지도록 트리를 유지한다. 이 성질을 만족하는 이진 트리를 이진 탐색 트리라고 부른다.
이진 탐색 트리를 통해 탐색할 때는 루트 노드부터 한 단계씩 아래로 내려가는 방식으로 진행한다. 데이터 원소가 현재 노드 값에 비해 작으면 왼쪽으로, 크다면 오른쪽 서브트리로 내려간다. 이렇게 진행하다 리프 노드까지 진행했는데도 원하는 값을 찾지 못한다면 해당 트리에 원하는 데이터 원소가 없다는 것을 뜻한다.
아래로 진행하면서 왼쪽 또는 오른쪽 서브트리를 선택하는 방식이므로 역시 재귀적인 성질을 활용한다는 것을 알 수 있다.
탐색 연산과 삽입/삭제 연산은 모두 평균적으로 O(log(n))에 비례하는 시간을 소모한다.
이진 탐색 트리는 key:value 형태로도 활용이 가능하다. 학생과 점수의 관계처럼, 점수(key)를 기준으로 트리를 생성하고 해당 key에 이어진 value값 정보를 알아낼 수도 있다.
이진 탐색 트리 연산 구현
class Node:
def __init__(self, key, data):
self.key = key
self.data = data
self.left = None
self.right = None
def insert(self, key, data):
if key < self.key: # 현재 노드보다 입력할 데이터가 작을 경우
if self.left:
self.left.insert(key, data) # 왼쪽으로 진행
else:
self.left = Node(key, data) # 왼쪽 노드가 없는 경우 그 곳에 데이터 입력
elif key > self.key: # 현재 노드보다 입력할 데이터가 클 경우
if self.right:
self.right.insert(key, data)
else:
self.right = Node(key, data)
else: # 입력할 값과 동일한 값이 이미 있는 경우
raise KeyError('Key %s already exists.' % key)
def lookup(self, key, parent=None):
if key < self.key:
if self.left:
return self.left.lookup(key, self)
else:
return None, None
elif key > self.key:
if self.right:
return self.right.lookup(key, self)
else:
return None, None
else:
return self, parent
def inorder(self):
traversal = []
if self.left:
traversal += self.left.inorder()
traversal.append(self)
if self.right:
traversal += self.right.inorder()
return traversal
def countChildren(self):
count = 0
if self.left:
count += 1
if self.right:
count += 1
return count
class BinSearchTree:
def __init__(self):
self.root = None
def insert(self, key, data):
if self.root:
self.root.insert(key, data)
else:
self.root = Node(key, data)
def lookup(self, key):
if self.root:
return self.root.lookup(key)
else:
return None, None
def remove(self, key):
node, parent = self.lookup(key)
if node:
nChildren = node.countChildren()
# The simplest case of no children
if nChildren == 0:
# 만약 parent 가 있으면
# node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
# parent.left 또는 parent.right 를 None 으로 하여
# leaf node 였던 자식을 트리에서 끊어내어 없앱니다.
if parent: # if parent.left == node 이렇게 비교해도 문제없다..
if parent.left:
if parent.left.key == key:
parent.left = None
else:
parent.right = None
else:
parent.right = None
# 만약 parent 가 없으면 (node 는 root 인 경우)
# self.root 를 None 으로 하여 빈 트리로 만듭니다.
else:
self.root = None
# When the node has only one child
elif nChildren == 1:
# 하나 있는 자식이 왼쪽인지 오른쪽인지를 판단하여
# 그 자식을 어떤 변수가 가리키도록 합니다.
if node.left:
child = node.left
else:
child = node.right
# 만약 parent 가 있으면
# node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
# 위에서 가리킨 자식을 대신 node 의 자리에 넣습니다.
if parent:
if parent.left:
if parent.left.key == key:
parent.left = child
else:
parent.right = child
else:
parent.right = child
# 만약 parent 가 없으면 (node 는 root 인 경우)
# self.root 에 위에서 가리킨 자식을 대신 넣습니다.
else:
self.root = child
# When the node has both left and right children
else:
parent = node
successor = node.right
# parent 는 node 를 가리키고 있고,
# successor 는 node 의 오른쪽 자식을 가리키고 있으므로
# successor 로부터 왼쪽 자식의 링크를 반복하여 따라감으로써
# 순환문이 종료할 때 successor 는 바로 다음 키를 가진 노드를,
# 그리고 parent 는 그 노드의 부모 노드를 가리키도록 찾아냅니다.
while successor.left:
parent = successor
successor = parent.left
# 삭제하려는 노드인 node 에 successor 의 key 와 data 를 대입합니다.
node.key = successor.key
node.data = successor.data
# 이제, successor 가 parent 의 왼쪽 자식인지 오른쪽 자식인지를 판단하여
# 그에 따라 parent.left 또는 parent.right 를
# successor 가 가지고 있던 (없을 수도 있지만) 자식을 가리키도록 합니다.
if parent.left == successor:
parent.left = successor.right # successor의 왼쪽 자식은 위 순환문의 조건때문에 존재하지 않음 (끝 왼쪽 자식까지 순환했기 때문)
else:
parent.right = successor.right
return True
else:
return False
def inorder(self):
if self.root:
return self.root.inorder()
else:
return []
def solution(x):
return 0
이 중 노드 삭제 연산인 remove()는 다소 복잡하다. 루트 노드 또는 내부 노드가 삭제되는 경우 다른 노드들을 옮겨서 다시 트리의 모습을 갖추도록 조정해야 하기 때문이다. 즉, 노드 삭제 이후 다시 이진 탐색 트리의 모양이 만족되도록 알고리즘을 구성해야 한다는 뜻이다.
다음과 같은 시나리오를 생각할 수 있다.
- 자식이 없는 노드 삭제: 리프노드이므로 해당 노드를 삭제 후 따로 처리가 필요없다.
- 자식이 하나만 있는 노드 삭제: 자식 노드가 부모 노드 자리로 옮겨온다. 똑같이 이진 탐색 트리의 조건이 만족된다.
- 자식이 둘인 노드 삭제: 삭제할 대상의 노드 값보다 한 칸 큰 값(석세서)으로 대체한다. 이후 석세서의 자식노드는 석세서의 부모 노드의 왼쪽 자식 노드로 계승된다. (석세서도 자식이 둘일 경우 똑같이 진행)
- 여기서 석세서는 삭제할 노드 기준 오른쪽 자식(큰 값)의 왼쪽 자식 노드의 끝 값(삭제 노드 보다는 크지만 그 중에 제일 작은 값)이다.
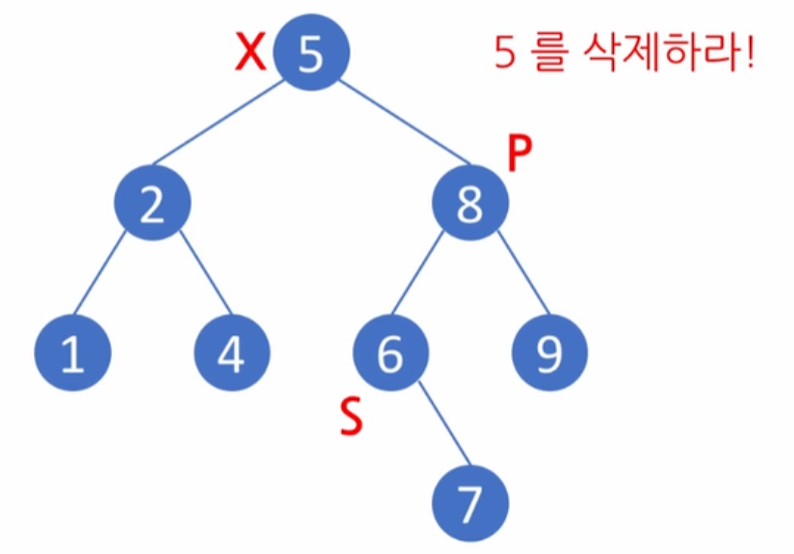
만약 삭제할 노드의 석세서까지 자식이 닿아있지 않을 경우, 바로 오른쪽 자식이 석세서의 역할을 한다.
이진 탐색 트리가 효과를 발휘할 수 없는 특수한 경우
이진 탐색 트리의 시간 복잡도 설명에서 평균적으로 O(log(n))의 시간이 걸린다고 했다. 바로 이진 탐색 트리가 효과가 없는 경우가 존재하기 때문이다. 만약 트리가 한 줄로 늘어서면 (즉, 모든 노드가 왼쪽 또는 오른쪽의 한 자식만을 가지는 경우) 노드의 개수가 n 이라 할 때 트리의 높이 (깊이) 또한 n이기 때문에, 이 경우 특정 원소를 탐색하면 이 탐색 연산의 복잡도는 선형 탐색 (linear search) 와 동일해진다.
이 한계점은, 이진 탐색 트리에 원소를 삽입함에 있어서 높이를 최소화하려는(트리의 좌우 균형을 유지하려는 노력)을 하지 않았기 때문이다. 이런 한계를 극복하기 위해서 이진 탐색 트리에 추가의 제약을 (만족해야 하는 성질을) 부가한 트리들이 있다. (아래의 트리들이 그 예시다.)
- AVL trees
- Red-black trees
힙 (Heaps)
힙도 이진 트리의 한 종류로, 이진 힙(Binary heap)이라고도 부른다. 힙은 데이터 원소들의 순서를 교묘하게 표현했다고 할 수 있다. 정렬에도 이용할 수 있는데, 힙을 이용해 데이터를 정렬하는 것을 힙 정렬(heap sort)이라고 한다.
힙에는 최대 힙과 최소 힙이 있다. 최대 힙과 최소 힙은 데이터 원소의 순서 기준이 내림차순이냐 오름차순이냐만 달라지고, 완전히 대칭되는 성질을 가지고 있다. 최대 힙 기준 힙의 성질은 아래와 같다.
- 루트 노드가 항상 최댓값을 가진다.
- 완전 이진 트리이다.
- 최대 힙 내의 임의의 노드를 루트로 하는 서브트리 또한 최대 힙이다. (재귀적 정의)
언뜻 이진 탐색 트리와 비슷해 보이지만, 조금 다른 특징을 가지고 있다. 최대 힙은 이진 탐색 트리와 달리 데이터가 완전히 크기 순서대로 정렬되어 있지는 않다. 또한, 이진 탐색 트리의 장점인 특정 원소를 빠르게 검색할 수 있는 것과 달리 최대 힙은 이러한 기능을 제공할 수 없다.
최대 힙의 장점은 '완전 이진 트리'여야 하는 제약 조건에 있다. n개의 노드로 이루어진 최대 힙의 높이는 항상 log(n) + 1(소수 부분 버림)으로 정해진다. 이 성질로 인해 데이터 원소의 삽입/삭제 시간도 항상 O(log(n))에 비례한다. 따라서, 어떤 최대 힙이 존재할 때, 이 힙으로부터 반복적으로 루트 노드를 삭제하면 (서 데이터 원소들을 꺼내면) 루트 노드에 들어 있는 키가 힙 내에서 최대임이 보장되어 있으므로 데이터를 내림차순으로 정렬할 수 있다.
최대 힙에서 원소의 삽입
최대 힙에서 원소를 삽입할 때에는 추가할 원소를 임시적으로 제일 마지막 순서에 배치한 다음, 부모 노드와 비교해 삽입 원소의 값이 더 클 경우 자리를 바꿔가는 방식으로 원소를 삽입하게 된다. 자식 노드보다 부모 노드가 크고, 따로 순서가 정해져 있지 않기 때문에 이런 방식으로 원소 삽입 알고리즘이 완성된다.
class MaxHeap:
def __init__(self):
self.data = [None]
def insert(self, item):
self.data.append(item)
ind = self.data.index(item)
if ind == 1: # 빈 리스트 (인덱스 0은 None이므로)
return True
while self.data[ind//2] < self.data[ind]: # 부모노드보다 현재노드 값이 더 클 경우
self.data[ind//2], self.data[ind] = self.data[ind], self.data[ind//2] # 자리 바꿔줌
ind = ind//2 # index값 업데이트
if ind == 1: # 루트 노드일 경우 반복문 종료
break
def solution(x):
return 0
최대 힙에서 원소의 삭제
최대 힙에서 원소를 삭제할 경우는 무조건 루트 노드(힙에서의 최댓값)가 제거되게 된다. 삭제된 부분은 임시로 트리의 제일 마지막 자리에 있는 노드가 대체하게 되고, 자식 노드들과 값을 비교해 아래로 이동하는 과정을 거치게 된다. 자식 노드가 둘 있을 경우 두 자식 노드 중 큰 값이 있는 쪽과 비교해 이동한다.
class MaxHeap:
def __init__(self):
self.data = [None]
def remove(self):
if len(self.data) > 1:
self.data[1], self.data[-1] = self.data[-1], self.data[1]
data = self.data.pop(-1)
self.maxHeapify(1)
else:
data = None
return data
def maxHeapify(self, i):
# 왼쪽 자식 (left child) 의 인덱스를 계산합니다.
left = i * 2
# 오른쪽 자식 (right child) 의 인덱스를 계산합니다.
right = i * 2 + 1
smallest = i
# 왼쪽 자식이 존재하는지, 그리고 왼쪽 자식의 (키) 값이 (무엇보다?) 더 큰지를 판단합니다.
if left < len(self.data) and self.data[left] > self.data[smallest]:
# 조건이 만족하는 경우, smallest 는 왼쪽 자식의 인덱스를 가집니다.
smallest = left
# 오른쪽 자식이 존재하는지, 그리고 오른쪽 자식의 (키) 값이 (무엇보다?) 더 큰지를 판단합니다.
if right < len(self.data) and self.data[right] > self.data[smallest]:
# 조건이 만족하는 경우, smallest 는 오른쪽 자식의 인덱스를 가집니다.
smallest = right
if smallest != i:
# 현재 노드 (인덱스 i) 와 최댓값 노드 (왼쪽 아니면 오른쪽 자식) 를 교체합니다.
self.data[i], self.data[smallest] = self.data[smallest], self.data[i]
# 재귀적 호출을 이용하여 최대 힙의 성질을 만족할 때까지 트리를 정리합니다.
self.maxHeapify(smallest)
def solution(x):
return 0'Minding's Programming > Knowledge' 카테고리의 다른 글
| [코딩 테스트/Python] 코딩 테스트에서 자주 사용되는 Python 표준 라이브러리 (1) | 2024.10.01 |
|---|---|
| [코딩테스트/Python] 코딩테스트 문제 유형 별 문제 풀이 방법 (1) | 2024.09.30 |
| [CS/Python] 자료구조 & 알고리즘 정리 - 연결 리스트, 스택, 후위 표기법 (0) | 2024.09.26 |
| [CS] 알고리즘의 복잡도 (시간 복잡도) (0) | 2024.09.26 |
| [CS/Python] 자료구조 & 알고리즘 정리 - 선형 배열, 정렬, 탐색, 재귀, 순열 (1) | 2024.09.26 |