자료구조는 왜 알아야 하는가?
ex) 리스트 내 최대값을 max() 함수를 통해 알아내고자 한다면, 리스트 전체 원소를 하나씩 읽어 비교하는 수 밖에 없다.
즉, 위의 예시의 경우 리스트의 크기가 커질수록 시간은 비례적으로 많이 걸릴 수 밖에 없다는 뜻이다. 이런 경우 자료구조를 잘 활용한다면, 낭비되는 시간을 획기적으로 줄일 수 있다.
알고리즘이란?
프로그래밍에서의 알고리즘은 주어진 문제의 해결을 위한 자료구조와 연산 방법에 대한 선택을 뜻한다. 같은 문제가 주어지더라도 어떤 자료구조와 연산 방법을 사용하느냐에 따라 효율성의 크기가 달라질 수 있다. 자료구조와 알고리즘이 깊은 관계를 가지고 있는 것도 이런 이유 때문이다. 알고리즘의 '선택'에는 자료구조에 대한 이해가 필수적이다.
선형 배열 (Linear Arrays)
선형 배열은 데이터들이 선처럼 일렬로 늘어진 형태를 말한다. Python에서는 list가 대표적이다. 이런 배열 형태에서는 왼쪽부터 index라는 이름으로 순서 번호가 붙게되고, 0부터 시작해 1씩 증가한다.
number = [1,2,3,4,5]
# 위 리스트의 index는 0,1,2,3,4
# 1번 인덱스에 해당하는 데이터는 2
number[1]
>>> 2리스트(배열) 연산 - 리스트 길이와 관계 없이 빠른 실행이 가능한 연산
(1)원소 덧붙이기
# 원소 덧붙이기(맨 마지막에 덧붙이기)
player = ['Kim', 'Park', 'Ryu', 'Roh']
player.append('Moon')
player
>>>['Kim', 'Park', 'Ryu', 'Roh', 'Moon']
(2)끝에서 꺼내기
# 마지막 원소 삭제
player = ['Kim', 'Park', 'Ryu', 'Roh', 'Moon']
player.pop()
player
>>>['Kim', 'Park', 'Ryu', 'Roh']
append()와 pop() 연산은 리스트의 길이와 관계없이 일정한 실행 시간이 소요된다. (O(1)의 시간 소요)
리스트(배열) 연산 - 리스트 길이와 비례해 실행 시간이 소요되는 연산
(1)원소 삽입하기
# 특정 위치에 원소 삽입(3번 인덱스 자리에 문자열 삽입)
player = ['Kim', 'Park', 'Ryu', 'Roh', 'Moon']
player.insert(3, 'Yang')
player
>>>['Kim', 'Park', 'Ryu', 'Yang', 'Roh', 'Moon']
(2)원소 삭제하기
# 특정 위치의 원소 삭제(2번 인덱스 원소 삭제)
player = ['Kim', 'Park', 'Ryu', 'Roh', 'Moon']
player.del(2)
player
>>>['Kim', 'Ryu', 'Yang', 'Roh', 'Moon']
insert()와 del() 연산은 리스트 내 특정 인덱스에 원소를 삽입하거나 삭제하는 연산이기 때문에, 리스트의 길이에 영향을 받는다. (O(n)의 연산시간)
원소 탐색하기
# 특정 원소의 인덱스 알아내기
player = ['Kim', 'Park', 'Ryu', 'Roh', 'Moon']
player.index('Roh')
>>>
3index() 연산을 이용하면 특정 원소의 위치를 알 수 있다. (원소가 2개 이상이라면 앞에 있는 원소의 인덱스가 반환된다.)
정렬(Sort)
정렬은 배열 내 원소를 정해진 기준에 따라 새로 늘어놓는 작업을 뜻한다. 정렬 알고리즘은 여러 종류가 있지만, Python의 list에서는 내장된 정렬 기능 두 가지를 이용해 쉽게 정렬 알고리즘을 구현할 수 있다.
- 파이썬 내장 함수 sorted()
- 리스트에 쓸 수 있는 메서드 .sort()
위 두 가지 방법의 다른 점은 sorted()는 함수, .sort()는 메서드라는 것이다. 함수는 독립적으로 존재할 수 있어 그 자체로 호출이 가능한 반면, 메서드는 클래스 또는 객체에 속해 있는 함수이기 때문에 해당 객체를 통해 호출할 수 있다.
# 오름차순 정렬(sorted 사용)
num = [3,2,1,4]
sorted(num)
>>> [1,2,3,4]
# 내림차순 정렬(sort() 사용)
num = [3,2,1,4]
num.sort(reverse=True)
num
>>> [4,3,2,1]
# 문자열을 길이 별로 정렬(lambda 함수 사용해 key 지정)
str_list = ['abc', 'ab', 'abcd']
sorted(str_list, key=lambda x: len(x))위와 같이 다양한 방법으로 정렬할 수 있으며, 특정 기준을 새로 정하고 싶을 때는 key를 지정해 새로운 기준을 만들 수도 있다.
탐색(Search)
(1) 선형 탐색(Linear Search)
선형 탐색은 앞에서부터 차례대로 원소를 탐색하여 원하는 원소를 찾는다. 이 경우 리스트의 길이에 비례하는 시간이 소요된다. (O(n)의 시간 소요)
(2) 이진 탐색(Binary Search)
이진 탐색은 크기 순으로 정렬되어 있다는 성질을 이용해 원하는 원소를 찾는 방식으로, 탐색하려는 리스트가 이미 정렬되어 있는 경우에만 적용 가능하다. 찾으려는 값과 중앙값을 비교해 크거나 작다면, 중앙값을 기준으로 찾는 원소로부터 멀어지는 쪽은 버릴 수 있기 때문에, 모든 원소를 탐색하지 않아도 된다.
일반적으로 이진 탐색이 선형 탐색보다 빠른 방법이긴 하지만, 항상 그런 것은 아니다. 정렬이 우선되어야 하기 때문인데, 정렬에 걸리는 시간이 더 길고 단 한번의 탐색만 필요하다면 선형 탐색을 선택하는 것도 방법일 것이다.
# 이진 탐색 알고리즘 구현
# 리스트 L에서 x에 해당하는 값의 인덱스를 찾기
def binary_search(L, x):
left = 0
right = len(L) - 1
while (left<=right): # left와 right가 같거나 right가 클때만 반복문 진행
middle = (left+right)//2
if x < L[middle]:
right = middle - 1 # x가 middle값보다 작을 경우 우측을 버림
elif x > L[middle]:
left = middle + 1 # x가 middle값보다 클 경우 좌측을 버림
else:
return middle
return -1
재귀 알고리즘 (recursive algorithms)
재귀 알고리즘은 재귀 함수를 사용해 문제를 풀이하는 방식이다. 재귀 함수는 하나의 함수에서 자신을 다시 호출하여 작업을 수행하는 함수를 뜻하는데, 이를 활용하면 같은 알고리즘을 반복적으로 적용해 문제를 풀 수 있다.
대표적인 예시로 자연수의 합 구하기와 같은 문제가 있다.
ex) 1부터 n까지의 모든 자연수의 합을 구하기
# 1부터 n까지의 모든 자연수의 합을 구하기
def sum(n):
return n +sum(n-1)위 경우 sum() 함수에서 sum(n-1) 함수를 재귀적으로 호출해 n부터 1씩 뺀 숫자를 더하고 있다. 하지만 이럴 경우 무한히 n-1의 합을 적용하게 된다. 답을 도출하는 시점이 주어져야 하기때문에, 하나의 수식을 추가할 필요가 있다.
# 1부터 n까지의 모든 자연수의 합을 구하기
def sum(n):
if n <= 1:
return n
else:
return n +sum(n-1)위 처럼 n이 1일때 재귀 알고리즘의 종결 조건을 추가해주어야 한다.
재귀 알고리즘은 인간의 입장에서는 이해하기 좋지만, 컴퓨터에 적용했을 때 효율성은 떨어질 수 있다. 함수를 다시 호출해야 하는 데 드는 비용이 있기 때문이다.
피보나치 순열 구현
# 재귀적 방법
def fibonacci(x):
if x == 0:
return 0
elif x == 1:
return 1
else:
return solution(x-1) + solution(x-2)
# 반복적 방법(반복문 사용)
def fibonacci(x):
a = 0
b = 1
for _ in range(x):
a, b = b, a+b # x번의 반복을 통해 a와 b를 갱신해 피보나치 수 계산
return a # x번째 피보나치 수 반환
재귀 알고리즘을 활용해 풀 수 있는 문제들
(1) 조합의 수 계산
n개의 서로 다른 원소에서 m개를 택하는 경우의 수를 구할 때 (ex. 5개의 원소 중 2개를 구하는 조합의 수)
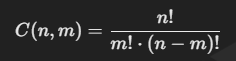
이 문제를 공식으로 나타내면 위와 같으며, 팩토리얼을 사용한다. Python에서는 math 라이브러리를 통해 팩토리얼을 쉽게 구할 수 있다. 예를 들어 5개 중 3개를 뽑는 조합의 수를 알아본다고 가정하자.
import math
def combination(n, m):
return math.factorial(n) // (math.factorial(m) * math.factorial(n - m))
이 문제를 재귀적 방법을 통해 구현할 수도 있다. 특정한 하나의 원소 입장에서 볼 때, 이 원소를 포함하는 경우와 그렇지 않은 경우를 따로 계산해서 더하면 된다.
C(n,m)=C(n−1,m−1)+C(n−1,m)
- 특정 원소를 선택하면 남은 n-1개의 원소 중에서 m-1개를 선택하는 경우로 나뉨
- 특정 원소를 선택하지 않으면 남은 n-1개의 원소 중에서 m개를 선택하는 경우로 나뉨
# 재귀적 방법으로 코드 구현
def combi(n, m):
if n == m:
return 1 # 전체를 선택하는 한 가지 방법밖에 없음
if m == 0:
return 0 # 선택지 없음
else:
return combi(n-1, m) + combi(n-1, m-1)하지만 이 경우 여러 개의 함수를 여러 번 호출하기 때문에, 효율성 측면에서는 좋지 않은 방법이다.
(2) 하노이의 탑 문제
효율성이 떨어지는 단점이 있지만, 재귀 알고리즘은 인간에게 직관적인 방법으로 구현할 수 있다는 장점이 있다. '하노이의 탑' 문제는 크기 순서로 쌓여 있는 원반을 한 막대에서 다른 막대로 옮기는 문제인데, 큰 원반일수록 아래로, 작은 원반일수록 위로 가야한다.
문제 풀이 예시
- 3개의 기둥이 있으며, 첫 번째 기둥에 크기가 서로 다른 n개의 원반이 있음.
- 모든 원반을 세 번째 기둥에 옮기되, 아래 규칙을 따라야 함.
규칙
- 한 번에 한 개의 원반만 이동 가능
- 더 큰 원반이 작은 원반 위에 놓일 수 없음
- 처음에는 모든 원반이 한 기둥에 쌓여 있으며, 원반의 크기는 아래에서 위로 작아짐.
해결 방법
- n-1개의 원반을 첫 번째 기둥에서 두 번째 기둥으로 옮김 (세 번째 기둥을 보조로 사용)
- 가장 큰 원반을 세 번째 기둥으로 옮김
- 두 번째 기둥에 있는 n-1개의 원반을 다시 세 번째 기둥으로 옮김 (첫 번째 기둥을 보조로 사용)
# n: 원반의 개수 / start: 시작기둥 / end: 옮기는 기둥 / aux: 보조 기둥(2번째)
def hanoi(n, start, end, aux):
if n == 1:
# 원반 1개를 시작 기둥에서 끝 기둥으로 이동
print(f"원반 1: {start} -> {end}")
return
# n-1개의 원반을 시작 기둥에서 보조 기둥으로 이동
hanoi(n-1, start, aux, end)
# 가장 큰 원반을 시작 기둥에서 끝 기둥으로 이동
print(f"원반 {n}: {start} -> {end}")
# n-1개의 원반을 보조 기둥에서 끝 기둥으로 이동
hanoi(n-1, aux, end, start)
# 예시 실행: 원반 3개를 첫 번째 기둥에서 세 번째 기둥으로 이동
hanoi(3, 'A', 'C', 'B')
>>>
원반 1: A -> C
원반 2: A -> B
원반 1: C -> B
원반 3: A -> C
원반 1: B -> A
원반 2: B -> C
원반 1: A -> C
(3) 피보나치 수열 문제
피보나치 수열도 재귀 알고리즘으로 구현할 수 있지만, 주어진 수가 커질수록 효율성이 많이 떨어진다는 단점이 있다. 재귀 알고리즘으로 풀이할 때, 주어진 수의 n-1, n-2에 해당하는 인자를 받는 함수가 호출되며 같은 함수가 반복적으로 호출되기 때문이다.
피보나치 수열 재귀 알고리즘 효율성 문제 해결 방법 - 메모이제이션
메모이제이션이라는 방법을 통해 재귀 알고리즘의 효율성 문제를 다소 개선할 수 있다. 이미 계산한 값은 딕셔너리에 저장해두고, 다시 계산할 필요없이 바로 사용할 수 있게 한다.
def fibonacci_memoization(n, memo={}):
if n in memo:
return memo[n]
if n == 0:
return 0
elif n == 1:
return 1
else:
memo[n] = fibonacci_memoization(n-1, memo) + fibonacci_memoization(n-2, memo)
return memo[n]
'Minding's Programming > Knowledge' 카테고리의 다른 글
| [CS/Python] 자료구조 & 알고리즘 정리 - 연결 리스트, 스택, 후위 표기법 (0) | 2024.09.26 |
|---|---|
| [CS] 알고리즘의 복잡도 (시간 복잡도) (0) | 2024.09.26 |
| [Linux/WSL] 간단한 리눅스 명령어 정리 (0) | 2024.07.18 |
| 카카오톡 메시지로 긍/부정어 감정 분석해보기 (재미로 보는 야구팬들의 감정 분석) (0) | 2024.07.15 |
| [Windows10/WSL2/Zsh] Windows에 zsh 설치하기 (0) | 2024.06.18 |