728x90
반응형
- 데이터셋 다운로드
github.com/WegraLee/deep-learning-from-scratch
WegraLee/deep-learning-from-scratch
『밑바닥부터 시작하는 딥러닝』(한빛미디어, 2017). Contribute to WegraLee/deep-learning-from-scratch development by creating an account on GitHub.
github.com
- 사진 출처
github.com/ExcelsiorCJH/DLFromScratch
ExcelsiorCJH/DLFromScratch
Deep Learning From Scratch. Contribute to ExcelsiorCJH/DLFromScratch development by creating an account on GitHub.
github.com
7.1 전체구조
- 이전의 신경망과 같이 계층을 조합하여 만들 수 있음
- 합성곱계층(Convolutional layer)과 풀링계층(Pooling layer)이 등장
- 완전연결층(fully conneted) : 인접하는 계층의 모든 뉴런과 결합된 신경망
- CNN의 구조 (합성곱과 풀링계층 추가)
7.2 합성곱 계층
- 패딩, 스트라이드 등 CNN 고유 용어 등장
7.2.1 완전연결 계층의 문제점
- 데이터의 형상이 무시됨 : 3차원 데이터를 1차원 데이터로 평탄화해야 함
- 이미지(3차원)의 형상에는 공간적 정보가 담겨져 있음
- 공간적으로 가까운 픽셀의 값은 비슷하거나, RGB의 각 채널은 서로 밀접연관 등의 패턴
- CNN의 합성곱계층은 형상을 유지 (3차원데이터 입력 / 출력)
- CNN에서는 합성곱 계층의 입출력 데이터를 특징 맵(feature map)이라고도 함 (입력특징맵 / 출력특징맵)
7.2.2 합성곱 연산
- 이미지 처리에서 말하는 필터 연산에 해당
- 예시 : 입력데이터는 세로,가로 방향의 형상가짐 (필터도 마찬가지)
- 입력은 (4,4), 필터는 (3,3), 출력은(2,2)의 형상
- 문헌에따라 필터를 커널이라고 지칭
- 합성곱연산은 필터의 윈도우를 일정 간격 이동해가며 입력데이터에 적용
- 입력과 필터에서 대응하는 원소끼리 곱한 후 그 총합 계산 (단일 곱셈-누산, FMA)

- Scipy의 2차원 합성곱함수(scipy.signal.convolved2d)를 이용하면 위의 예시와 다르게 나옴
- 같은 결과를 얻으려면 교차상관함수(scipy.signal.correlate2d)를 사용해야함
- 주어진 필터를 플리핑(flipping)하면 합성곱, 그렇지 않으면 교차상관
- 플리핑 : 원소들을 좌우,상하로 각 한번씩 뒤집는 것
- 딥러닝 라이브러리들의 합성곱함수들은 플리핑하지 않거나, 플리핑 여부를 인수로 받기도 함
- 편향까지 포함한 합성곱 연산
- 편향은 항상 하나(1,1)만 존재 = 모든 원소에 더함
7.2.3 패딩
- 합성곱 연산을 수행하기 전 입력 데이터 주변을 특정 값 (ex.0)으로 채우는 것
- 예시 : (4,4)크기의 입력데이터에 폭이 1인 패딩 적용

- (4,4) 입력데이터에 패딩 추가되어 (6,6)이 됨
- 패딩은 출력크기를 조정할 목적으로 사용
- 연산을 거칠 때 마다 출력의 형상은 계속해서 줄어들음
- 출력크기가 1이 되어버리면 합성곱연산 불가
- 입력데이터의 공간적크기를 고정한 채 다음계층에 전달가능
7.2.4 스트라이드
- 필터를 적용하는 위치의 간격
- 스트라이드를 2로 하면 필터적용 윈도우가 두 칸씩 이동

- 스트라이드를 키우면 출력크기는 작아짐
- 패딩, 스트라이드, 출력크기의 관계 수식화
- 입력크기(H,W) / 필터크기(FH, FW) / 출력크기(OH, OW) / 패딩 P / 스트라이드 S
- OH=(H+2P-FH)/S+1
- OW=(W+2P-FW)/S+1
- 수식들은 정수로 나눠떨어지는 값이어야 함
7.2.5 3차원 데이터의 합성곱 연산
- 채널 쪽으로 특징 맵이 여러 개 있을 때
- 입력데이터와 필터의 합성곱 연산을 채널마다 수행
- 연산수행 결과 더해서 출력 얻음

- 입력데이터의 채널 수와 필터의 채널 수가 같아야 함
- 필터 자체 크기는 원하는 값으로 설정가능 (모든 채널의 필터는 같은크기)
7.2.6 블록으로 생각하기
- 3차원 직육면체로 생각하면 이해 쉬움
- 3차원 데이터를 배열로 나타낼 때는 채널, 높이, 너비 순서 (C, H, W) / 필터 (C, FH, FW)
- 출력데이터는 한 장의 특징 맵 : 다수의 채널을 내보내려면 필터를 다수 사용

- 필터를 FN개 적용하면 출력 맵도 FN개 생성
- FN개의 맵을 모으면 (FN, OH, OW)인 블록 완성
- 합성곱 연산에서는 필터의 수도 고려해야 함
- 필터의 가중치 데이터는 4차원 데이터 (출력채널 수, 입력채널 수, 높이, 너비)
- 편향 추가

7.2.7 배치처리
- 각 계층을 흐르는 데이터의 차원을 하나 늘려 4차원 데이터로 저장
- (데이터 수, 채널 수, 높이, 너비)

- 주의 : 신경망에 4차원 데이터가 하나 흐를 때마다 데이터 N개에 대한 합성곱 연산수행
7.3 풀링계층
- 세로, 가로 방향의 공간을 줄이는 연산
- 최대 풀링(max pooling) : 최댓값을 구하는 연산
- 풀링의 원도우 크기와 스트라이드는 같은 값으로 설정하는 것이 보통
- 최대풀링의 예

7.3.1 풀링 계층의 특징
- 학습해야 할 매개변수가 없다
- 채널 수가 변하지 않는다
- 풀링연산은 채널마다 독립적으로 계산하기 때문에 입력채널 그대로 출력
- 입력의 변화에 영향을 적게 받는다 (강건하다)
- 입력 데이터의 차이를 풀링이 흡수해 사라지게 함
7.4 합성곱/풀링 계층 구현하기
7.4.1 4차원 배열
- CNN에서 계층 사이를 흐르는 데이터는 4차원
# 높이28, 너비28, 채널 1개인 데이터가 10개
import numpy as np
x = np.random.rand(10, 1, 28, 28) # 무작위로 데이터 생성
x.shape
>>> (10, 1, 28, 28)# 데이터 인덱스를 통한 접근
print(x[0].shape)
print(x[1].shape)
>>>
(1, 28, 28)
(1, 28, 28)# 첫번째 데이터의 첫 채널의 공간데이터에 접근
x[0, 0] # 또는 x[0][0]
>>>
array([[0.61206976, 0.84700886, 0.8283767 , 0.07469919, 0.65067234,
0.20880005, 0.76496379, 0.87379827, 0.04830922, 0.15357888,
0.97190819, 0.20289728, 0.82323917, 0.62009294, 0.5898003 ,
0.74319218, 0.91953033, 0.14464074, 0.88625752, 0.2942877 ,
0.99571249, 0.24535918, 0.02239101, 0.67893039, 0.51143285,
0.11055255, 0.61903003, 0.8351252 ],
...
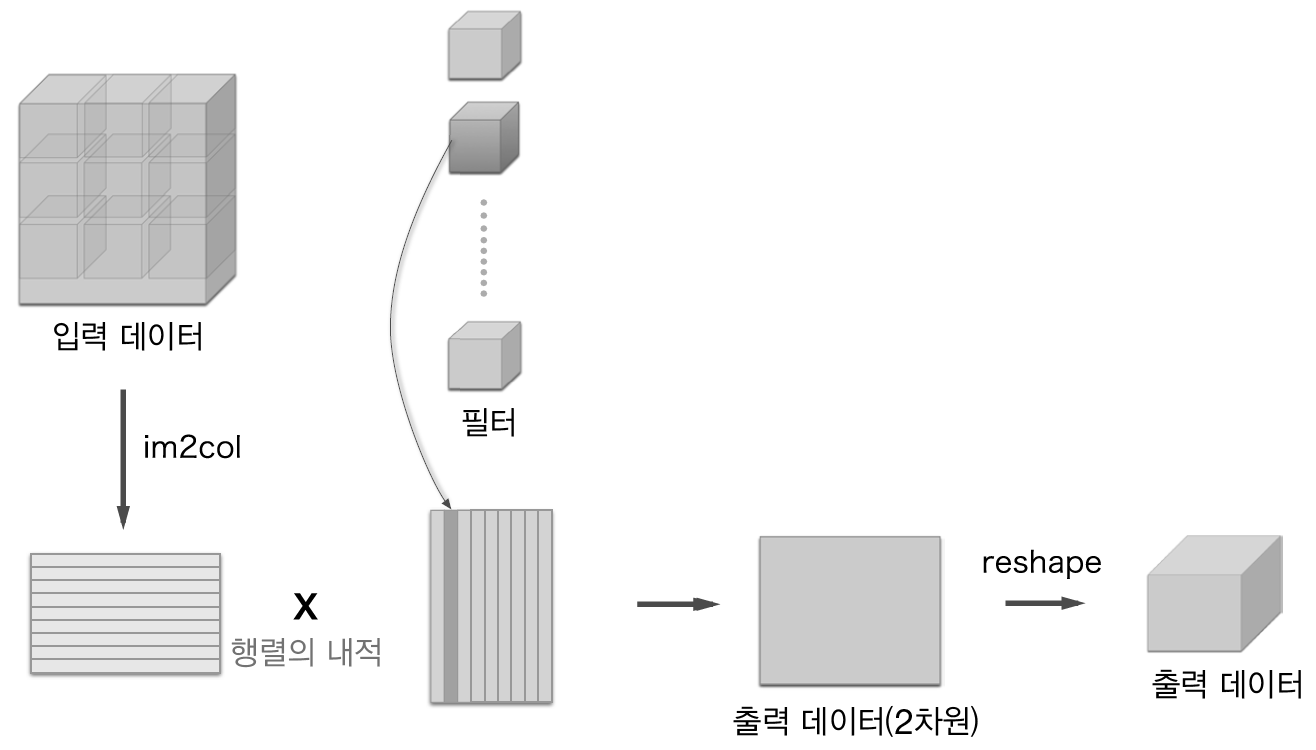
7.4.2 im2col로 데이터 전개하기
- for문 대신 im2col함수 사용하여 간단 구현
- 3차원 데이터에 im2col 적용하면 2차원 행렬로 바뀜

- 실제 상황에서는 필터 적용 영역이 겹치는 경우가 대부분
- 필터 적용 영역이 겹치게 되면 im2col로 전개한 후의 원소 수가 원래보다 많아짐 (메모리 더 많이 소비)
- 컴퓨터는 큰 행렬을 만들어 계산하는 데 탁월해 효율 높일 수 있음
- im2col 입력 데이터 전개 후 합성곱계층 필터 1열전개하고 행렬곱 계산
7.4.3 합성곱 계층 구현하기
- im2col의 인터페이스
- im2col(input_data, filter_h, filter_w, stride=1, pad=0)
- input_data : (데이터 수, 채널 수, 높이, 너비)의 입력데이터
- filter_h : 필터의 높이
- filter_w : 필터의 너비
- stride : 스트라이드
- pad : 패딩
# im2col 사용 구현
import sys, os
sys.path.append('/deep-learning-from-scratch')
from common.util import im2col
x1 = np.random.rand(1, 3, 7, 7) # 데이터 수, 채널 수, 높이, 너비
col1 = im2col(x1, 5, 5, stride=1, pad=0)
print(col1.shape)
x2 = np.random.rand(10, 3, 7, 7) # 데이터 10개
col2 = im2col(x2, 5, 5, stride=1, pad=0)
print(col2.shape)
>>>
(9, 75)
(90, 75)- 두 가지 경우 모두 2번째 차원의 원소는 75개
- 필터의 원소 수와 같음 (채널3, 5*5 데이터)
- 배치크기가 1일 때는 (9, 75) 10일 때는 10배인 (90, 75)
# 합성곱 계층 구현 - Convolution 클래스
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
out_h = int(1 + (H + 2*self.pad - FH) / self.stride)
out_w = int(1 + (W +2*self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad) # 입력데이터 전개
col_W = self.W.reshape(FN, -1).T # 필터 전개
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
return out- eshape 두 번째 인수 -1로 지정하면 다차원 배열의 원소 수가 변환 후에도 똑같이 유지되도록 묶어줌
- transpose함수를 이용해 출력데이터를 적절한 형상으로 바꾸어 줌
- 인덱스를 지정하여 축의 순서 변경
- 역전파에서는 im2col 대신 col2im 함수 사용
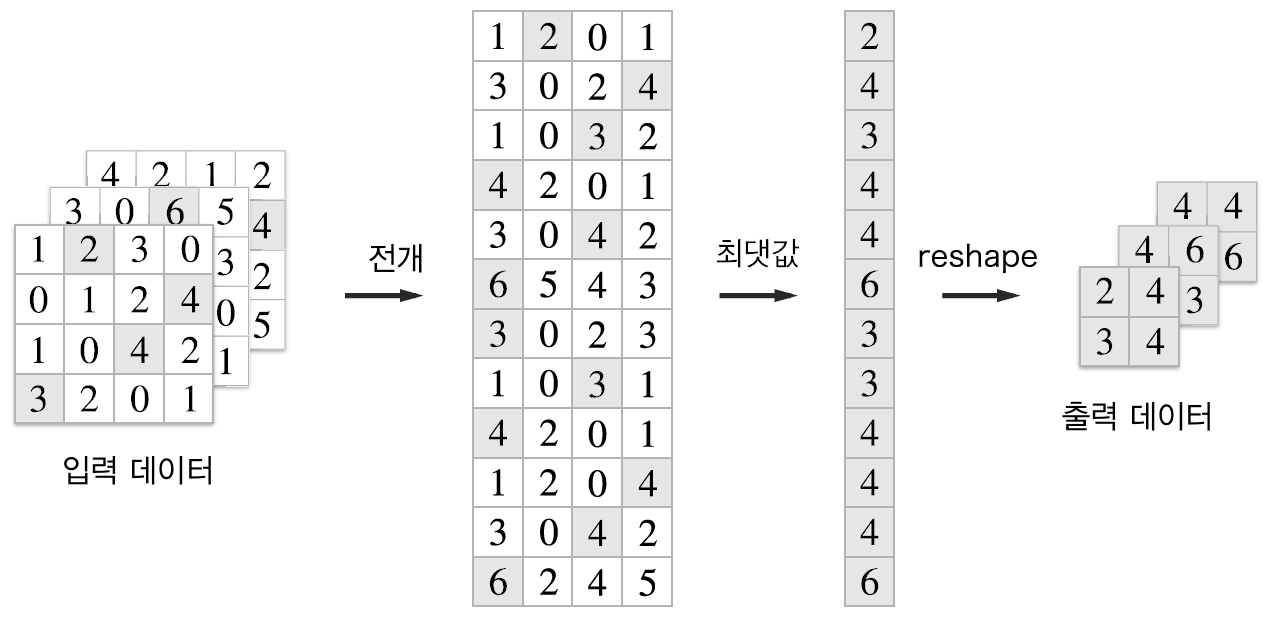
7.4.4 풀링 계층 구현하기
- 풀링의 경우에는 채널이 독립적이라는 점이 합성곱계층과 다른 점
- 전개 후 최댓값 구하고 적절한 형상으로 바꾸어줌
# 풀링 계층 구현
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
# 전개 (1)
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h*self.pool_w)
# 최댓값 (2)
out = np.max(col, axis=1) # 각 행마다 최댓값 도출
# 성형 (3)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
return out- 풀링 계층 구현의 세 단계
- 입력데이터 전개
- 행별 최댓값 구함
- 적절한 모양으로 성형
7.5 CNN 구현하기
- conv - relu - pool - affine - relu - affine - softmax 형태
- 초기화(__ init __)에서 받는 파라미터(인수)
- input_dim : 입력 데이터(채널 수, 높이, 너비)의 차원
- conv_param : 합성곱 계층의 하이퍼파라미터, 딕셔너리의 키는 다음과 같음
- filter_num : 필터 수
- filter_size : 필터 크기
- stride : 스트라이드
- pad : 패딩
- hidden_size : 은닉층(완전연결)의 뉴런 수
- output_size : 출력층(완전연결)의 뉴런 수
- weight_init_std : 초기화 때의 가중치 표준편차
- 합성곱계층의 하이퍼파라미터는 딕셔너리 형태로 주어짐
[CNN 구현 및 MNIST 학습코드는 너무 길어서 생략, 책과 데이터셋 참고]
7.6 CNN 시각화하기
7.6.1 1번째 층의 가중치 시각화하기
- 1번째 층의 합성곱 계층의 가중치는 (30, 1, 5, 5)
- 채널이 1개라는 것은 필터를 1채널의 회색조 이미지로 시각화 할 수 있다는 뜻
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
# from simple_convnet import SimpleConvNet
def filter_show(filters, nx=8, margin=3, scale=10):
"""
c.f. https://gist.github.com/aidiary/07d530d5e08011832b12#file-draw_weight-py
"""
FN, C, FH, FW = filters.shape
ny = int(np.ceil(FN / nx))
fig = plt.figure()
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
for i in range(FN):
ax = fig.add_subplot(ny, nx, i+1, xticks=[], yticks=[])
ax.imshow(filters[i, 0], cmap=plt.cm.gray_r, interpolation='nearest')
plt.show()
network = SimpleConvNet()
# 가중치 초기화(랜덤)
filter_show(network.params['W1'])
# 학습 후 가중치
network.load_params("/content/drive/MyDrive/deep-learning-from-scratch/ch07/params.pkl")
filter_show(network.params['W1'])
- 위의 사진이 학습전, 아래 사진이 학습 후의 필터
- 학습 전 필터는 무작위로 초기화되고 있어 흑백의 정도에 규칙성이 없음
- 학습을 마친 필터는 규칙성 있는 이미지
- 규칙성있는 필터는 에지(색상이 바뀐 경계선)와 볼륨(국소적으로 덩어리진 영역) 등 보고 있음
- 합성곱 계층의 필터는 에지나 블롭 등의 원시적인 정보 추출가능, 뒤 계층에 전달
7.6.2 층 깊이에 따른 추출 정보 변화
- 계층이 깊어질수록 추출되는 정보는 더 추상화 됨
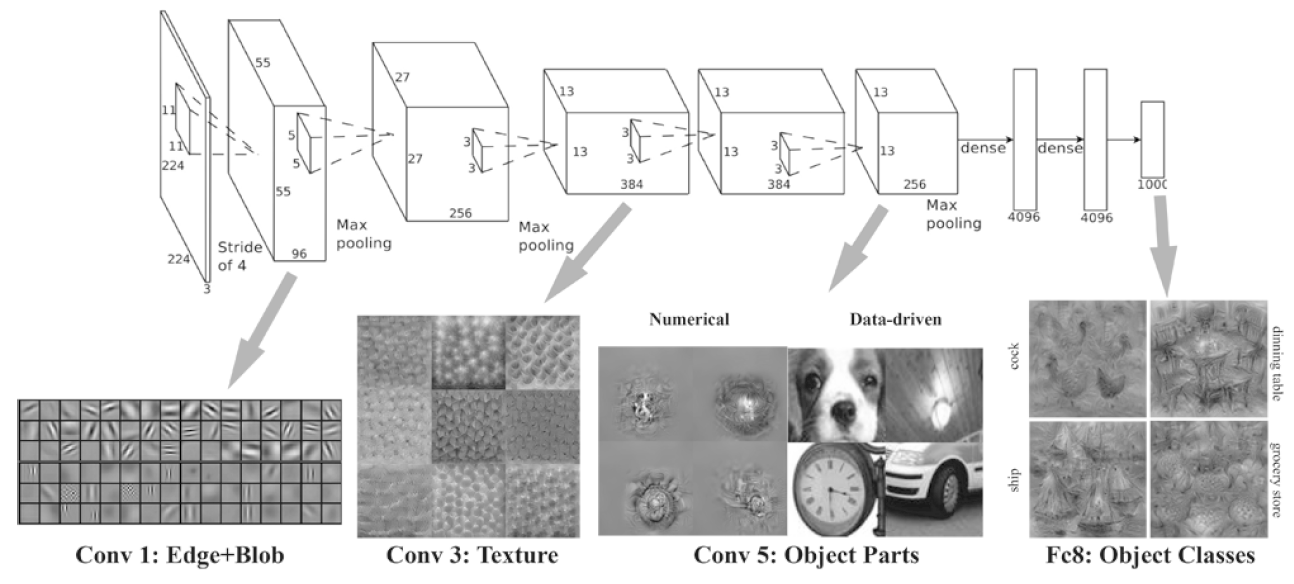
- 처음 층은 단순한 에지에 반응하고, 이어 텍스처에 반응하고, 더 복잡한 사물의 일부에 반응하도록 변화
7.7 대표적인 CNN
- LeNet과 AlexNet
7.7.1 LeNet
- 손글씨 숫자 인식 네트워크 (1998)
- 합성곱 계층과 풀링계층(단순히 원소를 줄이기만 하는 서브샘플링 계층)
- 마지막으로 완전연결계층 거치면서 결과 출력
- LeNet과 현재 CNN 비교
- 활성화 함수 : LeNet(sigmoid) / 현재(ReLU)
- 데이터 크기 줄이기 : LeNet(서브샘플링, 중간데이터 크기 줄임) / 현재(MaxPooling)
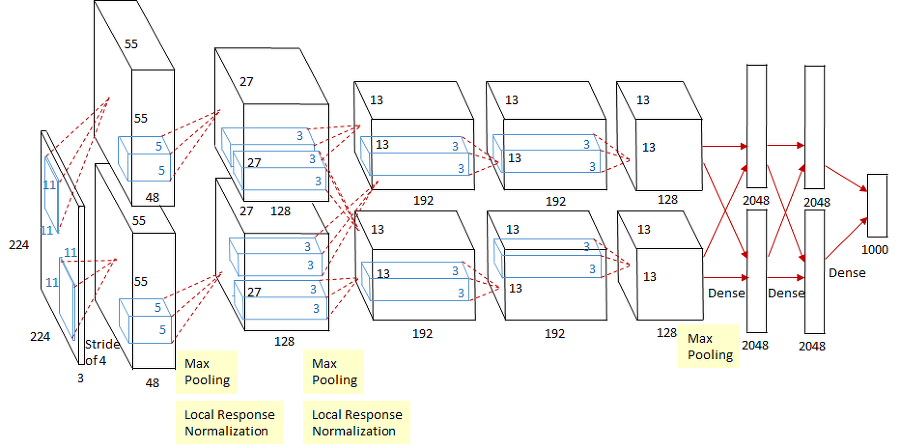
7.7.2 AlexNet
- LeNet과 비교해 바뀐 점
- 활성화 함수로 ReLU 사용
- LRN이라는 국소적 정규화 실시하는 계층 이용
- 드롭아웃 사용
- GPU계산 위해 병렬적인 구조로 설계
728x90
'Minding's Reading > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| [밑바닥부터 시작하는 딥러닝] CH.6 학습 관련 기술들 (0) | 2021.05.09 |
|---|---|
| [밑바닥부터 시작하는 딥러닝] CH.5 오차역전파법 (2) | 2021.05.09 |
| [밑바닥부터 시작하는 딥러닝] CH.4 신경망 학습 (0) | 2021.04.06 |
| [밑바닥부터 시작하는 딥러닝] CH.3 신경망 (0) | 2021.03.15 |
| [밑바닥부터 시작하는 딥러닝] CH.2 퍼셉트론 (2) | 2021.03.14 |
